Skip to contents

1. Matching and Weighting Methods

Manoj Khanal

Eli Lilly & Company

2024-04-12

Source: vignettes/match_weight_01_methods.Rmd
match_weight_01_methods.Rmd

Using external control in the analysis of clinical trial data can be challenging as the two data source may be heterogenous. In this document, we demonstrate the use of various matching and weighting techniques using readily available packages in R to adjust for imbalance in baseline covariates between the data sets.

We first load all of the libraries used in this tutorial.

To demonstrate the utility of the tools, we simulate data for a randomized controlled trial (RCT) and a dataset with external controls. We simulate a two arm trial where approximately 70%70\% of subjects receive the active treatment. The sample size for the RCT and external data is nD=600n_D=600 and nK=500n_K=500 respectively. In the RCT, we generate 55 continuous and 33 binary baseline covariates XX as follows:

  • The continuous variables are
    • Age (years): mean = 5555 and variance = 1515
    • Weight (lbs): mean = 150150 and variance = 1010
    • Height (inches): mean = 6565 and variance = 66
    • Biomarker1: mean = 5353 and variance = 55
    • Biomarker2: mean = 5050 and variance = 66
  • The categorical variables are
    • Smoker: Yes = 1 and No = 0. Proportion of Yes is 20%20\%.
    • Sex: Male = 1 and Female = 0. Proportion of Male is 80%80\%.
    • ECOG1: ECOG 1 = 1 and ECOG 0 = 0. Proportion of ECOG 1 is 30%30\%.

We simulate covariates with a correlation coefficient of 0.20.2 between all variables. For the continuous variables, we also specify the skewness and kurtosis to be 0.20.2 and 0.10.1, respectively, for all variables. Given the randomized nature of the RCT, subjects are assigned treatment at random.

Other variables in the simulated data include

  • The treatment indicator is
    • group: group = 1 is treatment and group = 0 is placebo.
  • The time to event variable is
    • time
  • The event indicator variable is
    • event: event = 1 is an event indicator and event = 0 is censored
  • The data indicator variable is
    • data: data = TRIAL indicating the trial data set

To generate the covariates, we first specify the sample sizes, number of continuous and categorical variables, the marginal moments of the covariates, and the correlation matrix. Note that rcorrvar2 requires the correlation matrix to be ordered as ordinal, continuous, Poisson, and Negative Binomial.

#Simulate correlated covariates
n_t <- 600 #Sample size in trial data
n_ec <- 500 #Sample size in external control data
k_cont <- 5 #Number of continuous variables
k_cat <- 3 #Number of categorical variables
means_cont_tc <- c(55,150,65,35,50) #Vector of means of continuous variables
vars_cont_tc <- c(15,10,6,5,6)
marginal_tc = list(0.2,0.8,0.3)
rho_tc <- matrix(0.2, 8, 8)
diag(rho_tc) <- 1
skews_tc <- rep(0.2,5)
skurts_tc <- rep(0.1,5)

Simulating trial data

After specifying the moments of the covariate distribution, we simulate the covariates using rcorrvar2 function from SimMultiCorrData package.

#Simulating covariates
trial.data <- rcorrvar2(n = n_t, k_cont = k_cont, k_cat = k_cat, k_nb = 0,
                        method = "Fleishman",  seed=1,
                        means = means_cont_tc, vars = vars_cont_tc, # if continuous variables
                        skews = skews_tc, skurts = skurts_tc, 
                        marginal=marginal_tc, rho = rho_tc)
#> 
#>  Constants: Distribution  1  
#> 
#>  Constants: Distribution  2  
#> 
#>  Constants: Distribution  3  
#> 
#>  Constants: Distribution  4  
#> 
#>  Constants: Distribution  5  
#> 
#> Constants calculation time: 0.003 minutes 
#> Intercorrelation calculation time: 0.002 minutes 
#> Error loop calculation time: 0 minutes 
#> Total Simulation time: 0.005 minutes
trial.data <- data.frame(cbind(id=paste("TRIAL",1:n_t,sep=""), trial.data$continuous_variables, 
                        ifelse(trial.data$ordinal_variables==1,1,0)))
colnames(trial.data) <- c("ID", "Age", "Weight","Height","Biomarker1","Biomarker2","Smoker", 
                          "Sex", "ECOG1")

We now simulate the survival outcome data using the Cox proportional hazards model (Cox 1972) in which the hazard function λ(t|𝐗,Z)\lambda(t|\boldsymbol X, Z) is given by λ(t|𝐗,Z)=λ0(t)exp{𝐗𝛃Trial+Zγ},\lambda(t|\boldsymbol X, Z)=\lambda_0(t) \exp\{\boldsymbol X \boldsymbol \beta_{Trial} + Z \gamma\},

where λ0(t)=2\lambda_0(t)=2 is the baseline hazard function and assumed to be constant, 𝐗\boldsymbol X is a matrix of baseline covariates, 𝛃Trial\boldsymbol \beta_{Trial} is a vector of covariate effects, ZZ is the treatment indicator, and γ\gamma is the treatment effect in terms of the log hazard ratio.

The survival function is given by S(t|𝐗,Z)=exp{−Λ(t|𝐗,Z)},S(t|\boldsymbol X, Z)=exp\{-\Lambda(t|\boldsymbol X, Z)\}, where Λ(t|𝐗,Z)=∫0tλ(u|𝐗,Z)du\Lambda(t|\boldsymbol X, Z)=\int_0^t\lambda(u|\boldsymbol X, Z)du. The time to event is generated using a inverse CDF method. The censoring time is generated independently from an exponential distribution with rate=1/4.

#Simulate survival outcome using Cox proportional hazards regression model
set.seed(1)
u <- runif(1)
lambda0 <- 2 #constant baseline hazard
#Simulate treatment indicator in the trial data
trial.data$group <- rbinom(n_t,1,prob=0.7)
beta <- c(0.3,0.1,-0.3,-0.2,-0.12,0.3,1,-1,-0.4)
times <- -log(u)/(lambda0*exp(as.matrix(trial.data[,-1])%*%beta)) #Inverse CDF method
cens.time <- rexp(n_t,rate=1/4) #Censoring time from exponential distribution
event <- as.numeric(times <= cens.time) #Event indicator. 0 is censored.
time <- pmin(times,cens.time)
#Combine trial data
trial.data <- data.frame(trial.data,time,event,data="TRIAL")

The first 10 observations in the RCT data is shown below.

ID Age Weight Height Biomarker1 Biomarker2 Smoker Sex ECOG1 group time event data
TRIAL1 55.51419 148.5092 65.63899 33.71898 55.26178 0 1 0 1 0.4089043 0 TRIAL
TRIAL2 49.93326 146.9441 63.44883 35.65828 45.50928 1 1 1 1 0.9721405 0 TRIAL
TRIAL3 58.51588 153.5435 70.53193 35.53710 55.89283 0 1 0 0 0.2956919 0 TRIAL
TRIAL4 48.61226 147.2873 64.10615 31.17663 55.80523 0 1 0 1 4.3111823 0 TRIAL
TRIAL5 51.84943 151.0312 62.16361 33.99677 48.01981 0 1 0 0 0.2644848 0 TRIAL
TRIAL6 51.81743 148.1115 68.69766 33.82398 47.32652 1 1 0 0 0.3103544 0 TRIAL
TRIAL7 58.04648 150.2572 71.35831 38.71276 50.68694 0 1 0 1 1.7177436 0 TRIAL
TRIAL8 50.72777 147.1815 64.55223 33.86884 49.31299 0 1 1 1 5.2652367 0 TRIAL
TRIAL9 55.16073 145.0733 63.84238 36.28519 50.27354 0 1 1 1 3.9595461 1 TRIAL
TRIAL10 54.85184 146.4757 65.59890 36.21950 47.12495 1 1 0 1 1.1788494 1 TRIAL

The censoring and event rate in the RCT data is

table(trial.data$event)/nrow(trial.data) 
#> 
#>         0         1 
#> 0.3883333 0.6116667

The distribution of the outcome time is

summary(trial.data$time)
#>     Min.  1st Qu.   Median     Mean  3rd Qu.     Max. 
#>  0.00771  0.35048  0.89904  1.61350  2.04652 21.27313

The summary of each of the baseline covariates and their standardized mean difference between treatment arms is shown below.

myVars <- c("Age", "Weight", "Height", "Biomarker1", "Biomarker2", "Smoker", "Sex",
          "ECOG1")

## Vector of categorical variables 
catVars <- c("Smoker", "Sex", "ECOG1", "group")

tab1 <- CreateTableOne(vars = myVars, strata = "group" , data = trial.data, factorVars = catVars)
print(tab1,smd=TRUE)
#>                         Stratified by group
#>                          0              1              p      test SMD   
#>   n                         178            422                           
#>   Age (mean (SD))         54.82 (4.00)   55.08 (3.83)   0.451       0.067
#>   Weight (mean (SD))     150.18 (3.02)  149.92 (3.24)   0.357       0.084
#>   Height (mean (SD))      65.30 (2.39)   64.88 (2.49)   0.056       0.173
#>   Biomarker1 (mean (SD))  35.26 (2.38)   34.89 (2.16)   0.066       0.161
#>   Biomarker2 (mean (SD))  50.21 (2.52)   49.91 (2.43)   0.181       0.119
#>   Smoker = 1 (%)             32 (18.0)      87 (20.6)   0.530       0.067
#>   Sex = 1 (%)               132 (74.2)     344 (81.5)   0.054       0.178
#>   ECOG1 = 1 (%)              44 (24.7)     139 (32.9)   0.057       0.182

Simulating external control data

The same set of covariates XX were simulated for the external control data as the RCT. The means, variances for continuous variables and proportion for categorical variables are modified for the external controls compared to the RCT according to the code below.

means_cont_ec <- c(55+2,150-2,65-2,35+2,50-2) #Vector of means of continuous variables
vars_cont_ec <- c(14,10,5,5,5)
marginal_ec = list(0.3,0.7,0.4)
ext.cont.data <- rcorrvar2(n = n_ec, k_cont = k_cont, k_cat = k_cat, k_nb = 0,
                        method = "Fleishman",  seed=3,
                        means = means_cont_ec, vars = vars_cont_ec, # if continuous variables
                        skews = skews_tc, skurts = skurts_tc, 
                        marginal=marginal_ec, rho = rho_tc)
#> 
#>  Constants: Distribution  1  
#> 
#>  Constants: Distribution  2  
#> 
#>  Constants: Distribution  3  
#> 
#>  Constants: Distribution  4  
#> 
#>  Constants: Distribution  5  
#> 
#> Constants calculation time: 0.003 minutes 
#> Intercorrelation calculation time: 0.001 minutes 
#> Error loop calculation time: 0 minutes 
#> Total Simulation time: 0.004 minutes
ext.cont.data <- data.frame(cbind(id=paste("EC",1:n_ec,sep=""), ext.cont.data$continuous_variables, 
                        ifelse(ext.cont.data$ordinal_variables==1,1,0)))
colnames(ext.cont.data) <- c("ID", "Age", "Weight","Height","Biomarker1","Biomarker2","Smoker", "Sex", "ECOG1")

The same generating mechanism used for the RCT data was used to simulate survival time for the external controls.

#Simulate survival outcome using Cox proportional hazards regression model
set.seed(1111)
u <- runif(1)
lambda0 <- 6 #constant baseline hazard
beta <- c(-0.27,-0.1,0.3,0.2,0.1,-0.31,-1,1)
times <- -log(u)/(lambda0*exp(as.matrix(ext.cont.data[,-1])%*%beta)) #Inverse CDF method
cens.time <- rexp(n_ec,rate=3) #Censoring time from exponential distribution
event <- as.numeric(times <= cens.time) #Event indicator. 0 is censored.
time <- pmin(times,cens.time)

#Simulate treatment indicator in the trial data
group <- 0

ext.cont.data <- data.frame(ext.cont.data,group,time,event,data="EC")

The first 10 observations in the external control data is shown below.

knitr::kable(head(ext.cont.data, 10))
ID Age Weight Height Biomarker1 Biomarker2 Smoker Sex ECOG1 group time event data
EC1 58.84399 149.2772 60.14479 41.13023 47.84936 1 0 0 0 0.1368416 1 EC
EC2 54.94800 142.9350 59.48098 33.54165 48.14581 1 1 1 0 0.0316781 0 EC
EC3 56.60197 144.2795 65.27178 37.10918 49.17472 0 1 0 0 0.0269829 0 EC
EC4 58.26515 144.3181 58.38123 35.80290 48.79969 0 1 0 0 0.5024074 0 EC
EC5 55.35845 151.2542 61.23105 34.81402 47.81858 1 1 1 0 0.1666448 1 EC
EC6 57.25913 147.4564 62.22442 34.45358 47.49526 1 1 1 0 0.0889376 0 EC
EC7 60.09491 143.2529 64.61370 38.69222 48.54340 0 1 0 0 0.0368207 0 EC
EC8 55.55786 149.6638 63.85947 37.91138 46.49153 0 1 1 0 0.0307342 1 EC
EC9 59.11727 143.3353 61.02850 35.18954 47.95672 0 1 0 0 0.0379876 0 EC
EC10 50.35400 141.1806 57.91327 34.52789 42.01203 1 1 0 0 0.2193177 1 EC

The censoring and event rate in the trial data is

table(ext.cont.data$event)/nrow(ext.cont.data) 
#> 
#>     0     1 
#> 0.328 0.672

The distribution of the outcome time is

summary(ext.cont.data$time)
#>      Min.   1st Qu.    Median      Mean   3rd Qu.      Max. 
#> 0.0000166 0.0211811 0.0542664 0.0995427 0.1207454 1.2824912

Merging trial and external control data

We can use bind_rows function to merge two datasets. Before using this function, we make sure that the column names for the same variables are consistent in the two datasets.

names(ext.cont.data)
#>  [1] "ID"         "Age"        "Weight"     "Height"     "Biomarker1"
#>  [6] "Biomarker2" "Smoker"     "Sex"        "ECOG1"      "group"     
#> [11] "time"       "event"      "data"
names(trial.data)
#>  [1] "ID"         "Age"        "Weight"     "Height"     "Biomarker1"
#>  [6] "Biomarker2" "Smoker"     "Sex"        "ECOG1"      "group"     
#> [11] "time"       "event"      "data"
#MS I recommend adding a statement that forces the colnames to be the same, like names(ex.cont.data)[1:10]=names(trial.data)[1:10]

Now, we merge the two datasets.

final.data <- data.frame(bind_rows(trial.data,ext.cont.data))
knitr::kable(head(final.data, 10))
ID Age Weight Height Biomarker1 Biomarker2 Smoker Sex ECOG1 group time event data
TRIAL1 55.51419 148.5092 65.63899 33.71898 55.26178 0 1 0 1 0.4089043 0 TRIAL
TRIAL2 49.93326 146.9441 63.44883 35.65828 45.50928 1 1 1 1 0.9721405 0 TRIAL
TRIAL3 58.51588 153.5435 70.53193 35.53710 55.89283 0 1 0 0 0.2956919 0 TRIAL
TRIAL4 48.61226 147.2873 64.10615 31.17663 55.80523 0 1 0 1 4.3111823 0 TRIAL
TRIAL5 51.84943 151.0312 62.16361 33.99677 48.01981 0 1 0 0 0.2644848 0 TRIAL
TRIAL6 51.81743 148.1115 68.69766 33.82398 47.32652 1 1 0 0 0.3103544 0 TRIAL
TRIAL7 58.04648 150.2572 71.35831 38.71276 50.68694 0 1 0 1 1.7177436 0 TRIAL
TRIAL8 50.72777 147.1815 64.55223 33.86884 49.31299 0 1 1 1 5.2652367 0 TRIAL
TRIAL9 55.16073 145.0733 63.84238 36.28519 50.27354 0 1 1 1 3.9595461 1 TRIAL
TRIAL10 54.85184 146.4757 65.59890 36.21950 47.12495 1 1 0 1 1.1788494 1 TRIAL 
knitr::kable(tail(final.data, 10))
ID Age Weight Height Biomarker1 Biomarker2 Smoker Sex ECOG1 group time event data
1091 EC491 54.63798 142.7690 62.33772 31.74800 46.58420 1 1 1 0 0.0880112 1 EC
1092 EC492 58.95356 155.2625 62.49057 39.68135 53.22807 0 0 0 0 0.0578393 0 EC
1093 EC493 56.71679 142.0092 65.47906 37.46290 47.76221 1 0 0 0 0.0157931 1 EC
1094 EC494 54.01146 142.2547 61.43211 36.80426 46.80182 0 1 1 0 0.0241804 1 EC
1095 EC495 54.97775 147.9758 59.52286 38.58231 46.74939 1 1 0 0 0.0937779 0 EC
1096 EC496 51.57175 150.7496 61.26278 33.03108 45.15747 1 1 0 0 0.1023785 0 EC
1097 EC497 55.43787 145.5014 60.75110 37.98437 53.90082 0 1 0 0 0.0636704 1 EC
1098 EC498 58.63598 148.5516 62.83803 41.17086 48.23983 1 0 0 0 0.0511597 1 EC
1099 EC499 59.18113 150.7839 64.16530 32.80313 47.07868 1 1 0 0 0.0295196 0 EC
1100 EC500 57.65147 149.4489 63.26176 35.64399 47.01619 0 1 0 0 0.0514581 0 EC

We examine the standardized mean difference for covariates between the RCT and external control data before conducting matching/weighting. Note that strata="data" in the following code.

tab2 <- CreateTableOne(vars = myVars, strata = "data" , data = final.data, factorVars = catVars)
print(tab2,smd=TRUE)
#>                         Stratified by data
#>                          EC             TRIAL          p      test SMD   
#>   n                         500            600                           
#>   Age (mean (SD))         57.00 (3.72)   55.00 (3.88)  <0.001       0.526
#>   Weight (mean (SD))     148.00 (3.15)  150.00 (3.17)  <0.001       0.633
#>   Height (mean (SD))      63.00 (2.23)   65.00 (2.47)  <0.001       0.850
#>   Biomarker1 (mean (SD))  37.00 (2.24)   35.00 (2.24)  <0.001       0.894
#>   Biomarker2 (mean (SD))  48.00 (2.23)   50.00 (2.46)  <0.001       0.853
#>   Smoker = 1 (%)            145 (29.0)     119 (19.8)   0.001       0.215
#>   Sex = 1 (%)               355 (71.0)     476 (79.3)   0.002       0.194
#>   ECOG1 = 1 (%)             195 (39.0)     183 (30.5)   0.004       0.179

Note that the standardized mean difference for all covariates is large. Next, we will conduct matching/weighting approach to reduce difference in baseline characteristics.

We also examine the standardized mean difference for covariates between the treated and control patients before conducting matching/weighting. Note that strata="group" in the following code.

tab2 <- CreateTableOne(vars = myVars, strata = "group" , data = final.data, factorVars = catVars)
print(tab2,smd=TRUE)
#>                         Stratified by group
#>                          0              1              p      test SMD   
#>   n                         678            422                           
#>   Age (mean (SD))         56.43 (3.91)   55.08 (3.83)  <0.001       0.348
#>   Weight (mean (SD))     148.57 (3.26)  149.92 (3.24)  <0.001       0.416
#>   Height (mean (SD))      63.60 (2.49)   64.88 (2.49)  <0.001       0.511
#>   Biomarker1 (mean (SD))  36.54 (2.40)   34.89 (2.16)  <0.001       0.723
#>   Biomarker2 (mean (SD))  48.58 (2.50)   49.91 (2.43)  <0.001       0.541
#>   Smoker = 1 (%)            177 (26.1)      87 (20.6)   0.045       0.130
#>   Sex = 1 (%)               487 (71.8)     344 (81.5)  <0.001       0.231
#>   ECOG1 = 1 (%)             239 (35.3)     139 (32.9)   0.472       0.049

Propensity scores overlap

Before applying the matching/weighting methods, we investigate the overlapping of propensity scores. The overlapping coefficient is only 0.190.19 indicating a very small overlap.

final.data$indicator <- ifelse(final.data$data=="TRIAL",1,0)
ps.logit <- glm(indicator ~ Age + Weight + Height + Biomarker1  + Biomarker2 + Smoker +
                            Sex +ECOG1, data = final.data,
                            family=binomial)
psfit=predict(ps.logit,type = "response",data=final.data)

ps_trial <- psfit[final.data$indicator==1] 
ps_extcont <- psfit[final.data$indicator==0]
overlap(list(ps_trial=ps_trial, ps_extcont=ps_extcont),plot=TRUE)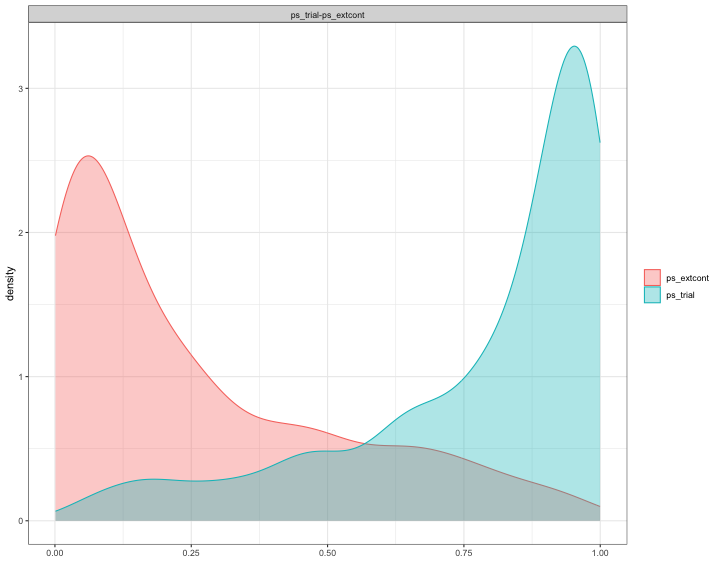
plot of chunk unnamed-chunk-28

plot of chunk unnamed-chunk-28 

#> $OV
#> [1] 0.3875297

Matching Methods

We will explore several matching methods to balance the balance the baseline characteristics between subjects in the RCT and external control data.

  • Matching methods
    • 1:1 Nearest Neighbor Propensity score matching with a caliper width of 0.2 of the standard deviation of the logit of the propensity score (PSML)
    • 1:1 Nearest Neighbor Propensity score matching with a caliper width of 0.2 of the standard deviation of raw propensity score (PSMR)
    • Genetic matching with replacement (GM)
    • 1:1 Genetic matching without replacement (GMW)
    • 1:1 Optimal matching (OM)

All of the matching methods can be conducted using the MatchIt package. The matching is conducted between the RCT subjects and external control subjects. Hence, we introduce a variable named indicator in final.data to represent the data source indicator.

final.data$indicator <- ifelse(final.data$data=="TRIAL",1,0)

PSML

This matching method is a variation of nearest neighbour or greedy matching that selects matches based on the difference in the logit of the propensity score, up to a certain distance (caliper) (Austin 2011). We selected a caliper width of 0.2 of the standard deviation of the logit of the propensity score, where the propensity score is estimated using a logistic regression.

m.out.nearest.ratio1.caliper.lps <- matchit(indicator ~ Age + Weight + Height + Biomarker1  + Biomarker2 + Smoker +
                                                        Sex +ECOG1, estimand="ATT",data = final.data, 
                                                        method="nearest",ratio=1,caliper=0.20,
                                                        distance="glm",link="linear.logit",replace=FALSE,
                                                        m.order="largest")
#> Warning: Fewer control units than treated units; not all treated units will get
#> a match.
summary(m.out.nearest.ratio1.caliper.lps)
#> 
#> Call:
#> matchit(formula = indicator ~ Age + Weight + Height + Biomarker1 + 
#>     Biomarker2 + Smoker + Sex + ECOG1, data = final.data, method = "nearest", 
#>     distance = "glm", link = "linear.logit", estimand = "ATT", 
#>     replace = FALSE, m.order = "largest", caliper = 0.2, ratio = 1)
#> 
#> Summary of Balance for All Data:
#>            Means Treated Means Control Std. Mean Diff. Var. Ratio eCDF Mean
#> distance          2.0386       -1.6416          1.8769     1.0922    0.4123
#> Age              55.0001       56.9985         -0.5151     1.0883    0.1497
#> Weight          150.0006      147.9990          0.6306     1.0170    0.1673
#> Height           65.0010       62.9998          0.8104     1.2222    0.2232
#> Biomarker1       34.9998       36.9999         -0.8948     0.9984    0.2397
#> Biomarker2       50.0003       47.9994          0.8138     1.2180    0.2254
#> Smoker            0.1983        0.2900         -0.2299          .    0.0917
#> Sex               0.7933        0.7100          0.2058          .    0.0833
#> ECOG1             0.3050        0.3900         -0.1846          .    0.0850
#>            eCDF Max
#> distance     0.6657
#> Age          0.2277
#> Weight       0.2493
#> Height       0.3247
#> Biomarker1   0.3717
#> Biomarker2   0.3463
#> Smoker       0.0917
#> Sex          0.0833
#> ECOG1        0.0850
#> 
#> Summary of Balance for Matched Data:
#>            Means Treated Means Control Std. Mean Diff. Var. Ratio eCDF Mean
#> distance          0.3084       -0.0768          0.1964     1.2651    0.0495
#> Age              55.9994       56.1273         -0.0330     1.2535    0.0200
#> Weight          149.0622      148.8328          0.0723     0.9531    0.0202
#> Height           63.9366       63.8937          0.0174     0.9519    0.0195
#> Biomarker1       35.8765       36.2704         -0.1762     1.1409    0.0574
#> Biomarker2       49.0364       48.8589          0.0722     1.0945    0.0225
#> Smoker            0.2455        0.2277          0.0448          .    0.0179
#> Sex               0.7857        0.7723          0.0331          .    0.0134
#> ECOG1             0.3304        0.3348         -0.0097          .    0.0045
#>            eCDF Max Std. Pair Dist.
#> distance     0.1786          0.1973
#> Age          0.0491          1.1372
#> Weight       0.0536          1.1005
#> Height       0.0625          0.9848
#> Biomarker1   0.1473          1.0799
#> Biomarker2   0.0536          0.9051
#> Smoker       0.0179          0.9628
#> Sex          0.0134          0.8489
#> ECOG1        0.0045          0.9987
#> 
#> Sample Sizes:
#>           Control Treated
#> All           500     600
#> Matched       224     224
#> Unmatched     276     376
#> Discarded       0       0
final.data$ratio1_caliper_weights_lps = m.out.nearest.ratio1.caliper.lps$weights

We now compare the SMD between the two datasets.

svy <- svydesign(id = ~0, data=final.data,weights = ~ratio1_caliper_weights_lps)
t1 <- svyCreateTableOne(vars = myVars, strata = "data" , data = svy, factorVars = catVars)
print(t1,smd=TRUE)
#>                         Stratified by data
#>                          EC             TRIAL          p      test SMD   
#>   n                      224.00         224.00                           
#>   Age (mean (SD))         56.13 (3.63)   56.00 (4.06)   0.725       0.033
#>   Weight (mean (SD))     148.83 (3.14)  149.06 (3.07)   0.434       0.074
#>   Height (mean (SD))      63.89 (2.14)   63.94 (2.08)   0.829       0.020
#>   Biomarker1 (mean (SD))  36.27 (2.10)   35.88 (2.25)   0.056       0.181
#>   Biomarker2 (mean (SD))  48.86 (2.12)   49.04 (2.21)   0.385       0.082
#>   Smoker = 1 (%)           51.0 (22.8)    55.0 (24.6)   0.657       0.042
#>   Sex = 1 (%)             173.0 (77.2)   176.0 (78.6)   0.733       0.032
#>   ECOG1 = 1 (%)            75.0 (33.5)    74.0 (33.0)   0.920       0.009

PSMR

This matching method is similar to PSML except the caliper width of 0.2 is based on the standard deviation of the propensity score scale (Stuart et al. 2011).

m.out.nearest.ratio1.caliper <- matchit(indicator ~ Age + Weight + Height + Biomarker1  + Biomarker2 + Smoker +
                                                    Sex +ECOG1, estimand="ATT",data = final.data, 
                                                    method = "nearest",  ratio = 1, caliper=0.2, replace=FALSE)
#> Warning: Fewer control units than treated units; not all treated units will get
#> a match.
summary(m.out.nearest.ratio1.caliper)
#> 
#> Call:
#> matchit(formula = indicator ~ Age + Weight + Height + Biomarker1 + 
#>     Biomarker2 + Smoker + Sex + ECOG1, data = final.data, method = "nearest", 
#>     estimand = "ATT", replace = FALSE, caliper = 0.2, ratio = 1)
#> 
#> Summary of Balance for All Data:
#>            Means Treated Means Control Std. Mean Diff. Var. Ratio eCDF Mean
#> distance          0.7827        0.2608          2.1517     0.8827    0.4123
#> Age              55.0001       56.9985         -0.5151     1.0883    0.1497
#> Weight          150.0006      147.9990          0.6306     1.0170    0.1673
#> Height           65.0010       62.9998          0.8104     1.2222    0.2232
#> Biomarker1       34.9998       36.9999         -0.8948     0.9984    0.2397
#> Biomarker2       50.0003       47.9994          0.8138     1.2180    0.2254
#> Smoker            0.1983        0.2900         -0.2299          .    0.0917
#> Sex               0.7933        0.7100          0.2058          .    0.0833
#> ECOG1             0.3050        0.3900         -0.1846          .    0.0850
#>            eCDF Max
#> distance     0.6657
#> Age          0.2277
#> Weight       0.2493
#> Height       0.3247
#> Biomarker1   0.3717
#> Biomarker2   0.3463
#> Smoker       0.0917
#> Sex          0.0833
#> ECOG1        0.0850
#> 
#> Summary of Balance for Matched Data:
#>            Means Treated Means Control Std. Mean Diff. Var. Ratio eCDF Mean
#> distance          0.5431        0.5011          0.1731     1.2229    0.0367
#> Age              56.0260       56.1310         -0.0271     1.1311    0.0181
#> Weight          148.9502      148.8880          0.0196     0.9491    0.0181
#> Height           64.1172       63.9245          0.0781     1.1794    0.0170
#> Biomarker1       35.9585       36.1764         -0.0975     1.1896    0.0426
#> Biomarker2       49.2512       48.9165          0.1361     1.4438    0.0344
#> Smoker            0.2266        0.2365         -0.0247          .    0.0099
#> Sex               0.7734        0.7734          0.0000          .    0.0000
#> ECOG1             0.3251        0.3498         -0.0535          .    0.0246
#>            eCDF Max Std. Pair Dist.
#> distance     0.1133          0.1743
#> Age          0.0443          1.1398
#> Weight       0.0640          1.0586
#> Height       0.0443          1.0077
#> Biomarker1   0.1182          0.9965
#> Biomarker2   0.0739          0.9127
#> Smoker       0.0099          0.9883
#> Sex          0.0000          0.3448
#> ECOG1        0.0246          0.9950
#> 
#> Sample Sizes:
#>           Control Treated
#> All           500     600
#> Matched       203     203
#> Unmatched     297     397
#> Discarded       0       0
final.data$ratio1_caliper_weights = m.out.nearest.ratio1.caliper$weights

We now compare the SMD between the two datasets.

svy <- svydesign(id = ~0, data=final.data,weights = ~ratio1_caliper_weights)
t1 <- svyCreateTableOne(vars = myVars, strata = "data" , data = svy, factorVars = catVars)
print(t1,smd=TRUE)
#>                         Stratified by data
#>                          EC             TRIAL          p      test SMD   
#>   n                      203.00         203.00                           
#>   Age (mean (SD))         56.13 (3.63)   56.03 (3.86)   0.777       0.028
#>   Weight (mean (SD))     148.89 (3.15)  148.95 (3.07)   0.840       0.020
#>   Height (mean (SD))      63.92 (2.15)   64.12 (2.34)   0.387       0.086
#>   Biomarker1 (mean (SD))  36.18 (2.07)   35.96 (2.26)   0.312       0.100
#>   Biomarker2 (mean (SD))  48.92 (2.07)   49.25 (2.49)   0.141       0.146
#>   Smoker = 1 (%)           48.0 (23.6)    46.0 (22.7)   0.814       0.023
#>   Sex = 1 (%)             157.0 (77.3)   157.0 (77.3)   1.000      <0.001
#>   ECOG1 = 1 (%)            71.0 (35.0)    66.0 (32.5)   0.600       0.052

GM

Genetic matching is a form of nearest neighbor matching where distances are computed using the generalized Mahalanobis distance, which is a generalization of the Mahalanobis distance with a scaling factor for each covariate that represents the importance of that covariate to the distance. A genetic algorithm is used to select the scaling factors. Matching is done with replacement, so an external control can be a matched for more than one patient in the treatment arm. Weighting is used to maintain the sample size in the treated arm (Sekhon 2008).

For a treated unit ii and a control unit jj, genetic matching uses the generalized Mahalanobis distance as δGMD(𝐱i,𝐱j,𝐖)=(𝐱i−𝐱j)′(𝐒−1/2)′𝐖(𝐒−1/2)(𝐱i−𝐱j)\delta_{GMD}(\mathbf{x}_i,\mathbf{x}_j, \mathbf{W})=\sqrt{(\mathbf{x}_i - \mathbf{x}_j)'(\mathbf{S}^{-1/2})'\mathbf{W}(\mathbf{S}^{-1/2})(\mathbf{x}_i - \mathbf{x}_j)} where 𝐱\mathbf{x} is a p×1p \times 1 vector containing the value of each of the pp included covariates for that unit, 𝐒−1/2\mathbf{S}^{-1/2} is the Cholesky decomposition of the covariance matrix 𝐒\mathbf{S} of the covariates, and 𝐖\mathbf{W} is a diagonal matrix with scaling factors ww on the diagonal (Greifer 2020). (w10…00w2…0⋮⋮⋱⋮00…wp) \begin{pmatrix} w_1 & 0 & \dots & 0 \\ 0 & w_2 & \dots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \dots & w_p \end{pmatrix}

If wk=1w_k=1 for all kk then the distance is the standard Mahalanobis distance. However, genetic matching estimates the optimal wkw_ks. The default is to maximize the smallest p-value among balance tests for the covariates in the matched sample (both Kolmogorov-Smirnov tests and t-tests for each covariate) (Greifer 2020).

m.out.genetic.ratio1 <- matchit(indicator ~ Age + Weight + Height + Biomarker1  + Biomarker2 + Smoker +
                                            Sex +ECOG1 ,replace=TRUE, estimand="ATT", 
                                            data = final.data, method = "genetic",  
                                            ratio = 1,pop.size=200)

summary(m.out.genetic.ratio1)
#> 
#> Call:
#> matchit(formula = indicator ~ Age + Weight + Height + Biomarker1 + 
#>     Biomarker2 + Smoker + Sex + ECOG1, data = final.data, method = "genetic", 
#>     estimand = "ATT", replace = TRUE, ratio = 1, pop.size = 200)
#> 
#> Summary of Balance for All Data:
#>            Means Treated Means Control Std. Mean Diff. Var. Ratio eCDF Mean
#> distance          0.7827        0.2608          2.1517     0.8827    0.4123
#> Age              55.0001       56.9985         -0.5151     1.0883    0.1497
#> Weight          150.0006      147.9990          0.6306     1.0170    0.1673
#> Height           65.0010       62.9998          0.8104     1.2222    0.2232
#> Biomarker1       34.9998       36.9999         -0.8948     0.9984    0.2397
#> Biomarker2       50.0003       47.9994          0.8138     1.2180    0.2254
#> Smoker            0.1983        0.2900         -0.2299          .    0.0917
#> Sex               0.7933        0.7100          0.2058          .    0.0833
#> ECOG1             0.3050        0.3900         -0.1846          .    0.0850
#>            eCDF Max
#> distance     0.6657
#> Age          0.2277
#> Weight       0.2493
#> Height       0.3247
#> Biomarker1   0.3717
#> Biomarker2   0.3463
#> Smoker       0.0917
#> Sex          0.0833
#> ECOG1        0.0850
#> 
#> Summary of Balance for Matched Data:
#>            Means Treated Means Control Std. Mean Diff. Var. Ratio eCDF Mean
#> distance          0.7827        0.7618          0.0860     1.0260    0.0379
#> Age              55.0001       55.1101         -0.0283     1.1784    0.0342
#> Weight          150.0006      149.3077          0.2183     1.2776    0.0561
#> Height           65.0010       64.9209          0.0324     1.1642    0.0145
#> Biomarker1       34.9998       35.3957         -0.1771     1.2578    0.0414
#> Biomarker2       50.0003       49.7966          0.0829     1.4752    0.0245
#> Smoker            0.1983        0.1933          0.0125          .    0.0050
#> Sex               0.7933        0.7933          0.0000          .    0.0000
#> ECOG1             0.3050        0.2483          0.1231          .    0.0567
#>            eCDF Max Std. Pair Dist.
#> distance     0.1950          0.1920
#> Age          0.0917          0.9201
#> Weight       0.1367          1.0483
#> Height       0.0683          0.1557
#> Biomarker1   0.1400          0.8230
#> Biomarker2   0.1150          0.6582
#> Smoker       0.0050          0.0125
#> Sex          0.0000          0.0000
#> ECOG1        0.0567          0.7747
#> 
#> Sample Sizes:
#>               Control Treated
#> All            500.       600
#> Matched (ESS)   43.22     600
#> Matched        151.       600
#> Unmatched      349.         0
#> Discarded        0.         0
final.data$genetic_ratio1_weights = m.out.genetic.ratio1$weights

We now compare the SMD between the two datasets.

svy <- svydesign(id = ~0, data=final.data,weights = ~genetic_ratio1_weights)
t1 <- svyCreateTableOne(vars = myVars, strata = "data" , data = svy, factorVars = catVars)
print(t1,smd=TRUE)
#>                         Stratified by data
#>                          EC             TRIAL          p      test SMD   
#>   n                      151.00         600.00                           
#>   Age (mean (SD))         55.11 (3.54)   55.00 (3.88)   0.830       0.030
#>   Weight (mean (SD))     149.31 (2.78)  150.00 (3.17)   0.111       0.232
#>   Height (mean (SD))      64.92 (2.27)   65.00 (2.47)   0.815       0.034
#>   Biomarker1 (mean (SD))  35.40 (1.98)   35.00 (2.24)   0.122       0.188
#>   Biomarker2 (mean (SD))  49.80 (2.01)   50.00 (2.46)   0.506       0.091
#>   Smoker = 1 (%)           29.2 (19.3)   119.0 (19.8)   0.924       0.013
#>   Sex = 1 (%)             119.8 (79.3)   476.0 (79.3)   1.000      <0.001
#>   ECOG1 = 1 (%)            37.5 (24.8)   183.0 (30.5)   0.346       0.127

GMW

We now consider genetic matching without replacement.

m.out.genetic.ratio1 <- matchit(indicator ~ Age + Weight + Height + Biomarker1  + Biomarker2 + Smoker +
                                            Sex +ECOG1 ,replace=FALSE, estimand="ATT", 
                                            data = final.data, method = "genetic",  
                                            ratio = 1,pop.size=200)
#> Warning: Fewer control units than treated units; not all treated units will get
#> a match.

summary(m.out.genetic.ratio1)
#> 
#> Call:
#> matchit(formula = indicator ~ Age + Weight + Height + Biomarker1 + 
#>     Biomarker2 + Smoker + Sex + ECOG1, data = final.data, method = "genetic", 
#>     estimand = "ATT", replace = FALSE, ratio = 1, pop.size = 200)
#> 
#> Summary of Balance for All Data:
#>            Means Treated Means Control Std. Mean Diff. Var. Ratio eCDF Mean
#> distance          0.7827        0.2608          2.1517     0.8827    0.4123
#> Age              55.0001       56.9985         -0.5151     1.0883    0.1497
#> Weight          150.0006      147.9990          0.6306     1.0170    0.1673
#> Height           65.0010       62.9998          0.8104     1.2222    0.2232
#> Biomarker1       34.9998       36.9999         -0.8948     0.9984    0.2397
#> Biomarker2       50.0003       47.9994          0.8138     1.2180    0.2254
#> Smoker            0.1983        0.2900         -0.2299          .    0.0917
#> Sex               0.7933        0.7100          0.2058          .    0.0833
#> ECOG1             0.3050        0.3900         -0.1846          .    0.0850
#>            eCDF Max
#> distance     0.6657
#> Age          0.2277
#> Weight       0.2493
#> Height       0.3247
#> Biomarker1   0.3717
#> Biomarker2   0.3463
#> Smoker       0.0917
#> Sex          0.0833
#> ECOG1        0.0850
#> 
#> Summary of Balance for Matched Data:
#>            Means Treated Means Control Std. Mean Diff. Var. Ratio eCDF Mean
#> distance          0.8753        0.2608          2.5336     0.2211    0.4823
#> Age              54.7088       56.9985         -0.5902     1.0304    0.1701
#> Weight          150.3086      147.9990          0.7276     0.9875    0.1960
#> Height           65.3230       62.9998          0.9408     1.2096    0.2597
#> Biomarker1       34.6396       36.9999         -1.0560     0.8539    0.2828
#> Biomarker2       50.2868       47.9994          0.9304     1.1739    0.2579
#> Smoker            0.1880        0.2900         -0.2558          .    0.1020
#> Sex               0.8060        0.7100          0.2371          .    0.0960
#> ECOG1             0.2920        0.3900         -0.2129          .    0.0980
#>            eCDF Max Std. Pair Dist.
#> distance      0.832          2.5336
#> Age           0.260          0.7405
#> Weight        0.292          0.7796
#> Height        0.382          0.9666
#> Biomarker1    0.434          1.0763
#> Biomarker2    0.398          0.9554
#> Smoker        0.102          0.6169
#> Sex           0.096          0.5433
#> ECOG1         0.098          0.4822
#> 
#> Sample Sizes:
#>           Control Treated
#> All           500     600
#> Matched       500     500
#> Unmatched       0     100
#> Discarded       0       0
final.data$genetic_ratio1_weights_no_replace = m.out.genetic.ratio1$weights

We now compare the SMD between the two datasets.

svy <- svydesign(id = ~0, data=final.data,weights = ~genetic_ratio1_weights_no_replace)
t1 <- svyCreateTableOne(vars = myVars, strata = "data" , data = svy, factorVars = catVars)
print(t1,smd=TRUE)
#>                         Stratified by data
#>                          EC             TRIAL          p      test SMD   
#>   n                      500.00         500.00                           
#>   Age (mean (SD))         57.00 (3.72)   54.71 (3.78)  <0.001       0.611
#>   Weight (mean (SD))     148.00 (3.15)  150.31 (3.13)  <0.001       0.736
#>   Height (mean (SD))      63.00 (2.23)   65.32 (2.46)  <0.001       0.989
#>   Biomarker1 (mean (SD))  37.00 (2.24)   34.64 (2.07)  <0.001       1.096
#>   Biomarker2 (mean (SD))  48.00 (2.23)   50.29 (2.41)  <0.001       0.985
#>   Smoker = 1 (%)          145.0 (29.0)    94.0 (18.8)  <0.001       0.241
#>   Sex = 1 (%)             355.0 (71.0)   403.0 (80.6)  <0.001       0.226
#>   ECOG1 = 1 (%)           195.0 (39.0)   146.0 (29.2)   0.001       0.208

OM

The optimal matching algorithm performs a global minimization of propensity score distance between the RCT subjects and matched external controls (Harris and Horst 2016). The criterion used is the sum of the absolute pair distances in the matched sample. Optimal pair matching and nearest neighbor matching often yield the same or very similar matched samples and some research has indicated that optimal pair matching is not much better than nearest neighbor matching at yielding balanced matched samples (Greifer 2020).

m.out.optimal.ratio1 <- matchit(indicator ~ Age + Weight + Height + Biomarker1  + Biomarker2 + Smoker +
                                            Sex +ECOG1 , estimand="ATT", 
                                            data = final.data, method = "optimal",  
                                            ratio = 1)
#> Warning: Fewer control units than treated units; not all treated units will get
#> a match.

summary(m.out.optimal.ratio1)
#> 
#> Call:
#> matchit(formula = indicator ~ Age + Weight + Height + Biomarker1 + 
#>     Biomarker2 + Smoker + Sex + ECOG1, data = final.data, method = "optimal", 
#>     estimand = "ATT", ratio = 1)
#> 
#> Summary of Balance for All Data:
#>            Means Treated Means Control Std. Mean Diff. Var. Ratio eCDF Mean
#> distance          0.7827        0.2608          2.1517     0.8827    0.4123
#> Age              55.0001       56.9985         -0.5151     1.0883    0.1497
#> Weight          150.0006      147.9990          0.6306     1.0170    0.1673
#> Height           65.0010       62.9998          0.8104     1.2222    0.2232
#> Biomarker1       34.9998       36.9999         -0.8948     0.9984    0.2397
#> Biomarker2       50.0003       47.9994          0.8138     1.2180    0.2254
#> Smoker            0.1983        0.2900         -0.2299          .    0.0917
#> Sex               0.7933        0.7100          0.2058          .    0.0833
#> ECOG1             0.3050        0.3900         -0.1846          .    0.0850
#>            eCDF Max
#> distance     0.6657
#> Age          0.2277
#> Weight       0.2493
#> Height       0.3247
#> Biomarker1   0.3717
#> Biomarker2   0.3463
#> Smoker       0.0917
#> Sex          0.0833
#> ECOG1        0.0850
#> 
#> Summary of Balance for Matched Data:
#>            Means Treated Means Control Std. Mean Diff. Var. Ratio eCDF Mean
#> distance          0.7410        0.2608          1.9801     0.9032    0.3589
#> Age              55.3043       56.9985         -0.4367     1.1079    0.1263
#> Weight          149.7031      147.9990          0.5369     0.9493    0.1424
#> Height           64.6469       62.9998          0.6670     1.0524    0.1886
#> Biomarker1       35.2375       36.9999         -0.7885     0.9722    0.2114
#> Biomarker2       49.5934       47.9994          0.6483     1.0178    0.1862
#> Smoker            0.2020        0.2900         -0.2207          .    0.0880
#> Sex               0.7760        0.7100          0.1630          .    0.0660
#> ECOG1             0.3360        0.3900         -0.1173          .    0.0540
#>            eCDF Max Std. Pair Dist.
#> distance      0.632          1.9801
#> Age           0.192          1.0969
#> Weight        0.220          1.1664
#> Height        0.286          1.1544
#> Biomarker1    0.342          1.2647
#> Biomarker2    0.296          1.1523
#> Smoker        0.088          0.9129
#> Sex           0.066          0.8940
#> ECOG1         0.054          1.1077
#> 
#> Sample Sizes:
#>           Control Treated
#> All           500     600
#> Matched       500     500
#> Unmatched       0     100
#> Discarded       0       0
final.data$optimal_ratio1_weights = m.out.optimal.ratio1$weights

We now compare the SMD between the two datasets.

svy <- svydesign(id = ~0, data=final.data,weights = ~optimal_ratio1_weights)
t1 <- svyCreateTableOne(vars = myVars, strata = "data" , data = svy, factorVars = catVars)
print(t1,smd=TRUE)
#>                         Stratified by data
#>                          EC             TRIAL          p      test SMD   
#>   n                      500.00         500.00                           
#>   Age (mean (SD))         57.00 (3.72)   55.30 (3.91)  <0.001       0.444
#>   Weight (mean (SD))     148.00 (3.15)  149.70 (3.07)  <0.001       0.548
#>   Height (mean (SD))      63.00 (2.23)   64.65 (2.29)  <0.001       0.728
#>   Biomarker1 (mean (SD))  37.00 (2.24)   35.24 (2.21)  <0.001       0.793
#>   Biomarker2 (mean (SD))  48.00 (2.23)   49.59 (2.25)  <0.001       0.712
#>   Smoker = 1 (%)          145.0 (29.0)   101.0 (20.2)   0.001       0.205
#>   Sex = 1 (%)             355.0 (71.0)   388.0 (77.6)   0.017       0.151
#>   ECOG1 = 1 (%)           195.0 (39.0)   168.0 (33.6)   0.076       0.112

Weighting Methods

We also explore several weighting approaches.

  • Weighting methods
    • Propensity score weighting based on a gradient boosted model (GBM)
    • Entropy balancing weighting (EB)
    • Inverse probability of treatment weighting (IPW)

GBM

The GBM (Gradient Boosting Machine) is a machine learning method which generates predicted values from a flexible regression model. It can adjust for a large number of covariates. The estimation involves an iterative process with multiple regression trees to capture complex and non-linear relationships. One of the most useful features of GBM for estimating the propensity score is that its iterative estimation procedure can be tuned to find the propensity score model leading to the best balance between treated and control groups, where balance refers to the similarity between different groups on their propensity score weighted distributions of pretreatment covariates (McCaffrey et al. 2013).

set.seed(1)


# Toolkit for Weighting and Analysis of Nonequivalent Groups
# https://cran.r-project.org/web/packages/twang/vignettes/twang.pdf

# Model includes non-linear effects and interactions with shrinkage to 
# avoid overfitting
                                                      
ps.AOD.ATT <- ps(indicator ~ Age + Weight + Height + Biomarker1  + Biomarker2 + Smoker +
                             Sex +ECOG1, data = final.data,
                             estimand = "ATT", interaction.depth=3, 
                             shrinkage=0.01, verbose = FALSE, n.trees = 7000, 
                             stop.method = c("es.mean","ks.max"))

# interaction.dept is the tree depth used in gradient boosting; loosely interpreted as 
# the maximum number of variables that can be included in an interaction

# n.trees is the maximum number of gradient boosting iterations to be considered. The
# more iterations allows for more nonlienarity and interactions to be considered.

# shrinkage is a numeric value between 0 and 1 denoting the learning rate. Smaller 
# values restrict the complexity that is added at each iteration of the gradient 
# boosting algorithm. A smaller learning rate requires more iterations (n.trees), but 
# adds some protection against model overfit. The default value is 0.01.

# windows()
# plot(ps.AOD.ATT, plot=5)
# 
# summary(ps.AOD.ATT)
# 
# # Relative influence
# summary(ps.AOD.ATT$gbm.obj, n.trees=ps.AOD.ATT$desc$ks.max.ATT$n.trees, plot=FALSE)
# 
# bal.table(ps.AOD.ATT)

final.data$weights_gbm <- ps.AOD.ATT$w[,1]

We now compare the SMD between the two datasets.

svy <- svydesign(id = ~0, data=final.data,weights = ~weights_gbm)
t1 <- svyCreateTableOne(vars = myVars, strata = "data" , data = svy, factorVars = catVars)
print(t1,smd=TRUE)
#>                         Stratified by data
#>                          EC             TRIAL          p      test SMD   
#>   n                      284.19         600.00                           
#>   Age (mean (SD))         54.93 (4.03)   55.00 (3.88)   0.902       0.018
#>   Weight (mean (SD))     148.84 (2.69)  150.00 (3.17)  <0.001       0.394
#>   Height (mean (SD))      64.27 (2.11)   65.00 (2.47)   0.002       0.317
#>   Biomarker1 (mean (SD))  35.61 (2.01)   35.00 (2.24)   0.002       0.285
#>   Biomarker2 (mean (SD))  49.57 (2.11)   50.00 (2.46)   0.081       0.188
#>   Smoker = 1 (%)           70.0 (24.6)   119.0 (19.8)   0.338       0.116
#>   Sex = 1 (%)             222.6 (78.3)   476.0 (79.3)   0.816       0.025
#>   ECOG1 = 1 (%)            85.7 (30.2)   183.0 (30.5)   0.950       0.007

EB

Entropy balancing is a weighting method to balance the covariates by assigning a scalar weight to each external control observations such that the reweighted groups satisfy a set of balance constraints that are imposed on the sample moments of the covariate distributions (Hainmueller 2012).

eb.out <- ebalance(final.data$indicator,final.data[,c(2:9)],max.iterations = 300)
#> Converged within tolerance
final.data$eb_weights <- rep(1,nrow(final.data))
final.data$eb_weights[final.data$indicator==0] <- eb.out$w

Note that the entropy balancing method failed to converge.

eb.out$converged
#> [1] TRUE

We now compare the SMD between the two datasets. By definition, the SMD after EB should be zero.

svy <- svydesign(id = ~0, data=final.data,weights = ~eb_weights)
t1 <- svyCreateTableOne(vars = myVars, strata = "data" , data = svy, factorVars = catVars)
print(t1,smd=TRUE)
#>                         Stratified by data
#>                          EC             TRIAL          p      test SMD   
#>   n                      600.00         600.00                           
#>   Age (mean (SD))         55.00 (3.68)   55.00 (3.88)   1.000      <0.001
#>   Weight (mean (SD))     150.00 (2.82)  150.00 (3.17)   1.000      <0.001
#>   Height (mean (SD))      65.00 (2.15)   65.00 (2.47)   1.000      <0.001
#>   Biomarker1 (mean (SD))  35.00 (1.49)   35.00 (2.24)   1.000      <0.001
#>   Biomarker2 (mean (SD))  50.00 (1.91)   50.00 (2.46)   1.000      <0.001
#>   Smoker = 1 (%)          119.0 (19.8)   119.0 (19.8)   1.000      <0.001
#>   Sex = 1 (%)             476.0 (79.3)   476.0 (79.3)   1.000      <0.001
#>   ECOG1 = 1 (%)           183.0 (30.5)   183.0 (30.5)   1.000      <0.001

IPW

The propensity score is defined as the probability of a patient being in a trial given the observed baseline covariates. We utilized the ATT weights, which are defined for the IPW as fixing the trial patients weight at unity, and external control patients as ê(x)/(1−ê(x))\hat{e}(x)/(1-\hat{e}(x)) where ê(x)\hat{e}(x) is estimated using a logistic regression model (Amusa, Zewotir, and North 2019).

ps.logit <- glm(indicator ~ Age + Weight + Height + Biomarker1  + Biomarker2 + Smoker +
                            Sex +ECOG1, data = final.data,
                            family=binomial)
psfit=predict(ps.logit,type = "response",data=final.data)

ps_trial <- psfit[final.data$indicator==1] 
ps_extcont <- psfit[final.data$indicator==0]

final.data$invprob_weights <- NA
final.data$invprob_weights[final.data$indicator==0] <- ps_extcont/(1-ps_extcont)
final.data$invprob_weights[final.data$indicator==1] <- ps_trial/ps_trial

We now compare the SMD between the two datasets.

svy <- svydesign(id = ~0, data=final.data,weights = ~invprob_weights)
t1 <- svyCreateTableOne(vars = myVars, strata = "data" , data = svy, factorVars = catVars)
print(t1,smd=TRUE)
#>                         Stratified by data
#>                          EC             TRIAL          p      test SMD   
#>   n                      522.38         600.00                           
#>   Age (mean (SD))         54.44 (4.03)   55.00 (3.88)   0.458       0.141
#>   Weight (mean (SD))     148.92 (2.76)  150.00 (3.17)   0.002       0.364
#>   Height (mean (SD))      64.65 (2.26)   65.00 (2.47)   0.311       0.147
#>   Biomarker1 (mean (SD))  35.38 (1.80)   35.00 (2.24)   0.077       0.185
#>   Biomarker2 (mean (SD))  49.83 (2.11)   50.00 (2.46)   0.589       0.076
#>   Smoker = 1 (%)           90.5 (17.3)   119.0 (19.8)   0.568       0.064
#>   Sex = 1 (%)             419.5 (80.3)   476.0 (79.3)   0.849       0.024
#>   ECOG1 = 1 (%)           121.3 (23.2)   183.0 (30.5)   0.158       0.165

Next we will investigate balance plots.

covs <- data.frame(final.data[,c("Age","Weight","Height","Biomarker1","Biomarker2","Smoker","Sex","ECOG1")])
data_with_weights <- final.data

Balance Plots for Matching Methods

We now conduct a balance diagnostic by considering SMD plot. The x-axis of the plot represent the absolute value of the SMD and y-axis represent the list of all covariates. SMD greater than 0.10.1 can be considered a sign of imbalance (Zhang et al. 2019). Hence, we put a threshold of 0.10.1 in the plot with a vertical dashed line.

love.plot(covs, 
          treat=data_with_weights$data,
          weights = list(NNMPS=data_with_weights$ratio1_caliper_weights,
                         NNMLPS=data_with_weights$ratio1_caliper_weights_lps,
                         OPTM=data_with_weights$optimal_ratio1_weights,
                         GENMATCH=data_with_weights$genetic_ratio1_weights,
                         GENMATCHW=data_with_weights$genetic_ratio1_weights_no_replace),
          thresholds=0.1 ,binary="std",shapes = c("circle filled"),
          line=FALSE,estimand="ATT",abs=TRUE,
          sample.names = c("PSMR", 
                           "PSML", 
                           "OM",
                           "GM",
                           "GMW"),
          title="Covariate Balance after matching methods",
          s.d.denom="pooled")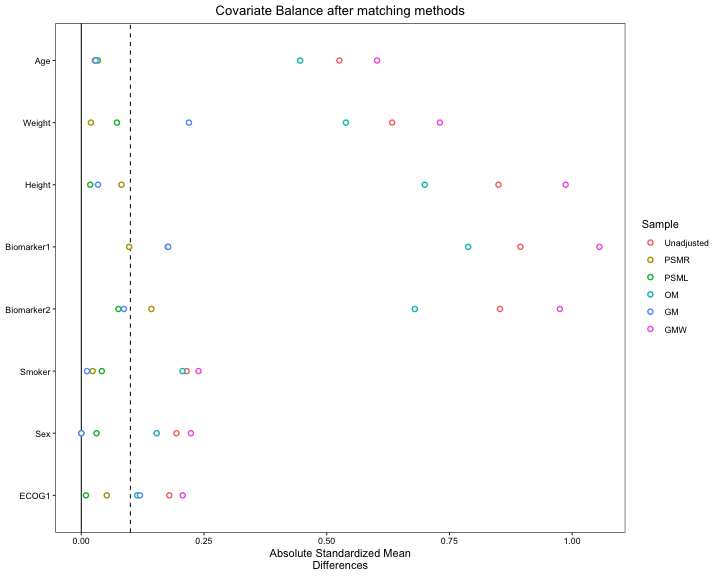
plot of chunk unnamed-chunk-61

plot of chunk unnamed-chunk-61

Balance Plots for Weighting Methods 

love.plot(covs, 
          treat=data_with_weights$data,
          weights = list(EB=data_with_weights$eb_weights,
                         IPW=data_with_weights$invprob_weights,
                         GBM=data_with_weights$weights_gbm),
          thresholds=0.1 ,binary="std",shapes = c("circle filled"),
          line=FALSE,estimand="ATT",abs=TRUE,
          sample.names = c("EB", 
                           "IPW", 
                           "GBM"),
          title="Covariate Balance after weighting methods",
          s.d.denom="pooled")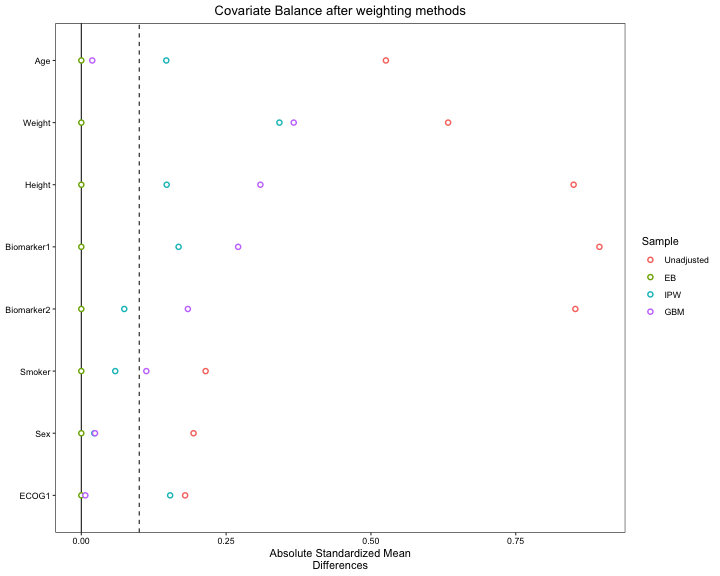
plot of chunk unnamed-chunk-62

plot of chunk unnamed-chunk-62

We now investigate the effective sample size (ESS) in the trial and external control cohort.

#External control
ess.PSML.extcont <- (sum(data_with_weights$ratio1_caliper_weights_lps[data_with_weights$indicator==0]))^2/
                     sum((data_with_weights$ratio1_caliper_weights_lps[data_with_weights$indicator==0])^2)

ess.PSMR.extcont <- (sum(data_with_weights$ratio1_caliper_weights[data_with_weights$indicator==0]))^2/
                    sum((data_with_weights$ratio1_caliper_weights[data_with_weights$indicator==0])^2)

ess.OM.extcont <- (sum(data_with_weights$optimal_ratio1_weights[data_with_weights$indicator==0]))^2/
                  sum((data_with_weights$optimal_ratio1_weights[data_with_weights$indicator==0])^2)

ess.GM.extcont <- (sum(data_with_weights$genetic_ratio1_weights[data_with_weights$indicator==0]))^2/
                  sum((data_with_weights$genetic_ratio1_weights[data_with_weights$indicator==0])^2)

ess.eb.extcont <- (sum(data_with_weights$eb_weights[data_with_weights$indicator==0]))^2/
                  sum((data_with_weights$eb_weights[data_with_weights$indicator==0])^2)

ess.ipw.extcont <- (sum(data_with_weights$invprob_weights[data_with_weights$indicator==0]))^2/
                   sum((data_with_weights$invprob_weights[data_with_weights$indicator==0])^2)

ess.gbm.extcont <- (sum(data_with_weights$weights_gbm[data_with_weights$indicator==0]))^2/
                   sum((data_with_weights$weights_gbm[data_with_weights$indicator==0])^2)

ess.genetic.extcont <- (sum(data_with_weights$genetic_ratio1_weights[data_with_weights$indicator==0]))^2/
                       sum((data_with_weights$genetic_ratio1_weights[data_with_weights$indicator==0])^2)

ess.genetic.no.replace.extcont <- (sum(data_with_weights$genetic_ratio1_weights_no_replace[data_with_weights$indicator==0]))^2/
                       sum((data_with_weights$genetic_ratio1_weights_no_replace[data_with_weights$indicator==0])^2)
#Trial
ess.PSML.trial <- (sum(data_with_weights$ratio1_caliper_weights_lps[data_with_weights$indicator==1]))^2/
                  sum((data_with_weights$ratio1_caliper_weights_lps[data_with_weights$indicator==1])^2)

ess.PSMR.trial <- (sum(data_with_weights$ratio1_caliper_weights[data_with_weights$indicator==1]))^2/
                  sum((data_with_weights$ratio1_caliper_weights[data_with_weights$indicator==1])^2)

ess.OM.trial <- (sum(data_with_weights$optimal_ratio1_weights[data_with_weights$indicator==1]))^2/
                sum((data_with_weights$optimal_ratio1_weights[data_with_weights$indicator==1])^2)

ess.GM.trial <- (sum(data_with_weights$genetic_ratio1_weights[data_with_weights$indicator==1]))^2/
                sum((data_with_weights$genetic_ratio1_weights[data_with_weights$indicator==1])^2)

ess.eb.trial <- (sum(data_with_weights$eb_weights[data_with_weights$indicator==1]))^2/
                sum((data_with_weights$eb_weights[data_with_weights$indicator==1])^2)

ess.ipw.trial <- (sum(data_with_weights$invprob_weights[data_with_weights$indicator==1]))^2/
                 sum((data_with_weights$invprob_weights[data_with_weights$indicator==1])^2)

ess.gbm.trial <- (sum(data_with_weights$weights_gbm[data_with_weights$indicator==1]))^2/
                 sum((data_with_weights$weights_gbm[data_with_weights$indicator==1])^2)

ess.genetic.trial <- (sum(data_with_weights$genetic_ratio1_weights[data_with_weights$indicator==1]))^2/
                     sum((data_with_weights$genetic_ratio1_weights[data_with_weights$indicator==1])^2)
ess.genetic.no.replace.trial <- (sum(data_with_weights$genetic_ratio1_weights_no_replace[data_with_weights$indicator==1]))^2/
                     sum((data_with_weights$genetic_ratio1_weights_no_replace[data_with_weights$indicator==1])^2)
out.ess <- data.frame(Unadjusted=c(length(which(final.data$data=="TRIAL")),length(which(final.data$data=="EC"))),
           PSML=c(ess.PSML.trial,ess.PSML.extcont),
           PSMR=c(ess.PSMR.trial,ess.PSMR.extcont),
           OM=c(ess.OM.trial,ess.OM.extcont),
           GM=c(ess.genetic.trial,ess.genetic.extcont),
           GMW=c(ess.genetic.no.replace.trial,ess.genetic.no.replace.extcont),
           EB=c(ess.eb.trial,ess.eb.extcont),
           IPW=c(ess.ipw.trial,ess.ipw.extcont),
           GBM=c(ess.gbm.trial,ess.gbm.extcont))

rownames(out.ess) <- c("Trial","External Control")

Note: After applying the matching methods, some patients in RCT were excluded. For demonstration purpose in this article, we will also exclude RCT patients that were not matched in the Bayesian outcome model. However, in reality we may keep the full sample size in RCT and discounting could be done at the second stage with power prior and commensurate prior. Before, moving to the next stage of Bayesian borrowing, ESS also needs to be taken into account.

The ESS for each cohort using different methods are shown below.

out.ess
#>                  Unadjusted PSML PSMR  OM        GM GMW        EB       IPW
#> Trial                   600  224  203 500 600.00000 500 600.00000 600.00000
#> External Control        500  224  203 500  43.21729 500  27.69881  43.69827
#>                        GBM
#> Trial            600.00000
#> External Control  73.21273

We also investigate the histogram of the weights for external control patients and the effective sample size (ESS).

par(mfrow=c(2,2))
hist(data_with_weights$eb_weights[data_with_weights$indicator==0],main=paste("EB \n ESS=",round(ess.eb.extcont),sep=""),xlab="Weight")
hist(data_with_weights$invprob_weights[data_with_weights$indicator==0],main=paste("IPW\n ESS=",round(ess.ipw.extcont),sep=""),xlab="Weight")
hist(data_with_weights$weights_gbm[data_with_weights$indicator==0],main=paste("GBM \n ESS=",round(ess.gbm.extcont),sep=""),xlab="Weight")
hist(data_with_weights$genetic_ratio1_weights[data_with_weights$indicator==0],main=paste("GM \n ESS=",round(ess.genetic.extcont),sep=""),xlab="Weight")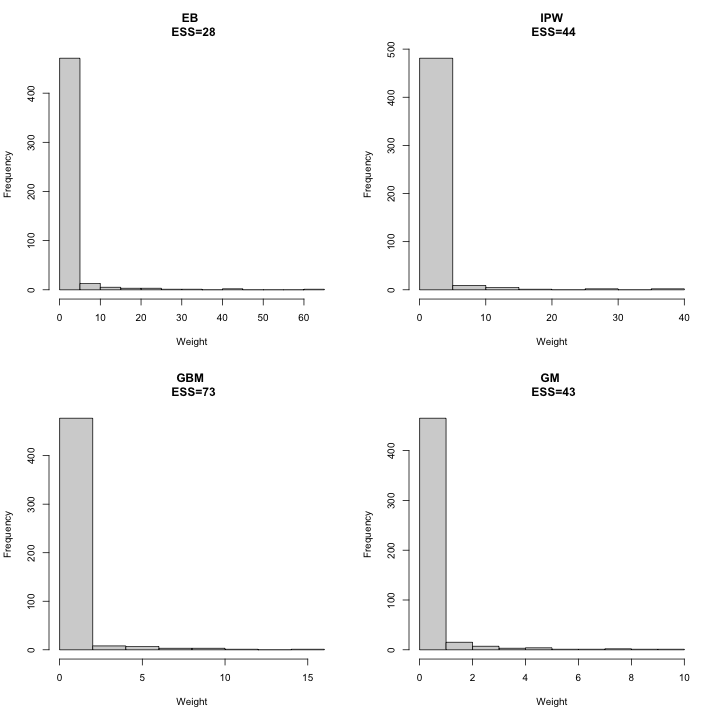
plot of chunk unnamed-chunk-67

plot of chunk unnamed-chunk-67

Selection of matching/weighting methods

Based on the standardized difference mean plot, PSML, PSMR, and GM can be the methods for selection. In terms of ESS, the PSML has the highest sample size of 215215 in both trial and external control data.

References

Amusa, Lateef, Temesgen Zewotir, and Delia North. 2019. “Examination of Entropy Balancing Technique for Estimating Some Standard Measures of Treatment Effects: A Simulation Study.” Electronic Journal of Applied Statistical Analysis 12 (2): 491–507.
Austin, Peter C. 2011. “Optimal Caliper Widths for Propensity-Score Matching When Estimating Differences in Means and Differences in Proportions in Observational Studies.” Pharmaceutical Statistics 10 (2): 150–61.
Cox, David R. 1972. “Regression Models and Life-Tables.” Journal of the Royal Statistical Society: Series B (Methodological) 34 (2): 187–202.
Greifer, Noah. 2020. “An Update on the MatchIt Package in r.” Last Modified December 8: 2020.
Hainmueller, Jens. 2012. “Entropy Balancing for Causal Effects: A Multivariate Reweighting Method to Produce Balanced Samples in Observational Studies.” Political Analysis 20 (1): 25–46.
Harris, Heather, and S Jeanne Horst. 2016. “A Brief Guide to Decisions at Each Step of the Propensity Score Matching Process.” Practical Assessment, Research, and Evaluation 21 (1): 4.
McCaffrey, Daniel F, Beth Ann Griffin, Daniel Almirall, Mary Ellen Slaughter, Rajeev Ramchand, and Lane F Burgette. 2013. “A Tutorial on Propensity Score Estimation for Multiple Treatments Using Generalized Boosted Models.” Statistics in Medicine 32 (19): 3388–3414.
Sekhon, Jasjeet S. 2008. “Multivariate and Propensity Score Matching Software with Automated Balance Optimization: The Matching Package for r.” Journal of Statistical Software, Forthcoming.
Stuart, EA, G King, K Imai, and D MatchIt Ho. 2011. “Nonparametric Preprocessing for Parametric 368 Causal Inference.” Journal of Statistical Software 369.
Zhang, Zhongheng, Hwa Jung Kim, Guillaume Lonjon, Yibing Zhu, et al. 2019. “Balance Diagnostics After Propensity Score Matching.” Annals of Translational Medicine 7 (1).