stats4phc

Introduction to stats4phc

This package provides functions for performance evaluation for the prognostic value of predictive models when the outcomes of interest are binary. We will describe 3 aspects that support such a performance evaluation:

• Predictiveness curves
• Calibration
• Sensitivity and specificity

To begin with, let’s align on terminology.

Terminology

Below we define the terms that will be used across the article:

• outcome: the true observation of the quantity of interest;

• score:

  • either a raw value (e.g. a biomarker) for the purpose of measuring (or approximating) the outcome,

  • or a prediction score given by a predictive model, where the outcome was modeled as the response;

• estimate: output of a statistical methodology, where score is used as independent variable and outcome as a dependent variable.

Predictiveness curves

Predictiveness curves are an insightful visualization to assess the inherent ability of prognostic models to provide predictions to individual patients. Cumulative versions of predictiveness curves represent positive predictive values (PPV) and 1 - negative predictive values (1 - NPV) and are also informative if the eventual goal is to use a cutoff for clinical decision making.

You can use riskProfile function to visualize and assess all these quantities.

Here is an example:

library(stats4phc)

# Read in example data
auroc <- read.csv(system.file("extdata", "sample.csv", package = "stats4phc"))
rscore <- auroc$predicted_calibrated
truth <- as.numeric(auroc$actual)

p <- riskProfile(outcome = truth, score = rscore)
p$plot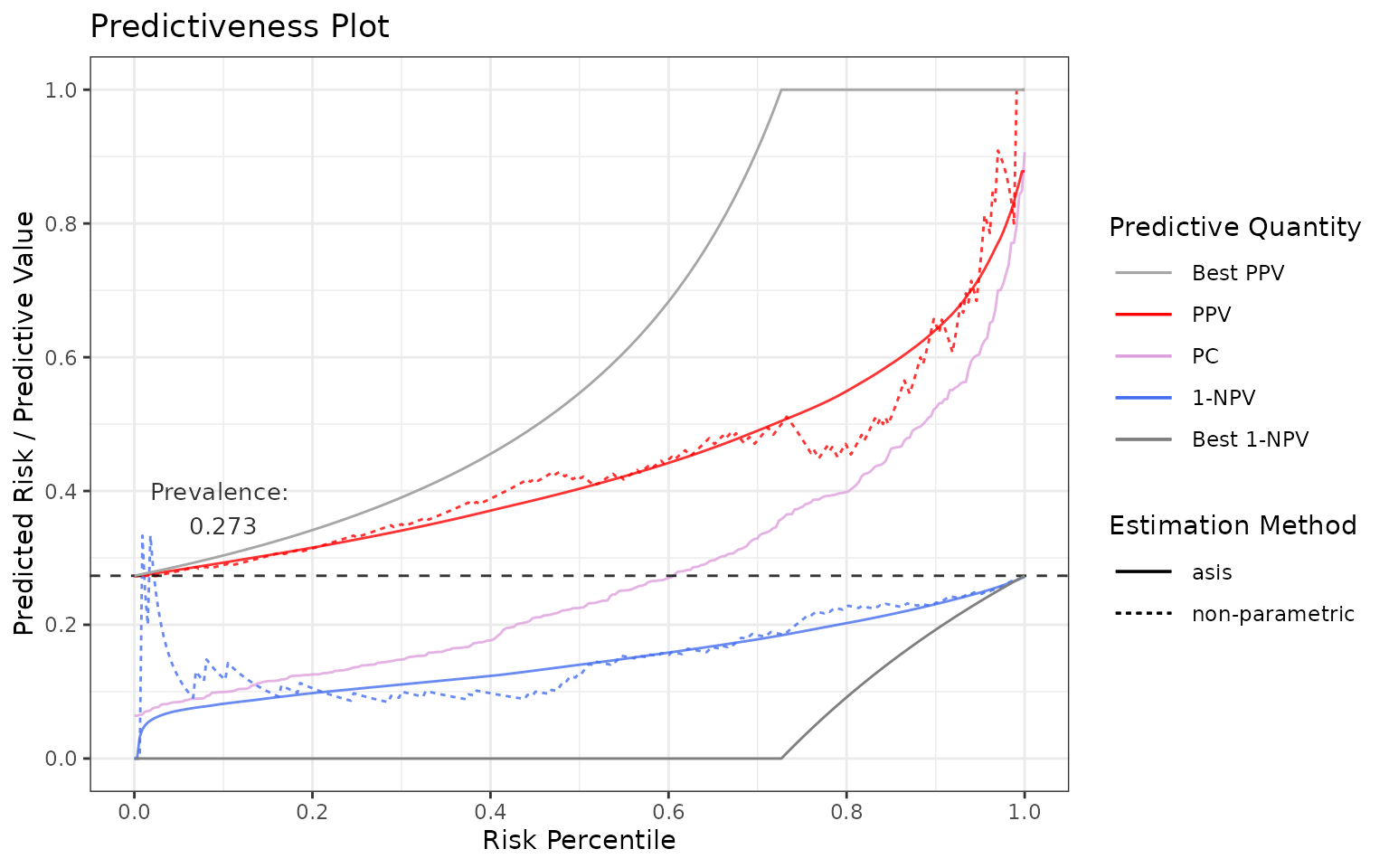

head(p$data)

## # A tibble: 6 × 7
##   method   score percentile outcome estimate pv    pvValue
##   <chr>    <dbl>      <dbl>   <dbl>    <dbl> <chr>   <dbl>
## 1 asis   NA         0            NA   0.0640 PC         NA
## 2 asis    0.0640    0.00300       0   0.0640 PC         NA
## 3 asis    0.0654    0.00601       0   0.0654 PC         NA
## 4 asis    0.0659    0.00901       1   0.0659 PC         NA
## 5 asis    0.0702    0.0120        0   0.0702 PC         NA
## 6 asis    0.0709    0.0150        0   0.0709 PC         NA

There is an extensive documentation of this function with examples if you run ?riskProfile.

To briefly highlight the functionalities:

• Use the methods argument to specify the desired estimation method (see the last section) or use "asis" for no estimation.

• You can adjust the prevalence by setting prev.adj to the desired amount.

• show.nonparam.pv controls whether to show/hide the non-parametric estimation of PPV, 1-NPV, and NPV.

• show.best.pv controls whether to show/hide the theoretically best possible PPV, 1-NPV, NPV.

• Use include argument to specify what quantities to show:

  • PC = predictiveness curve

  • PPV = positive predictive value

  • NPV = negative predictive value

  • 1-NPV = 1 - negative predictive value

• plot.raw sets whether to plot raw values or percentiles.

• rev.order sets whether to reverse the order of the score (useful if higher score refers to lower outcome).

• The output is the plot itself and the underlying data.

Calibration

Calibration is the assessment of systematic bias in a score. Visually, when plotting score on the x-axis vs. outcomes on the y-axis, the model is calibrated if points are centered around the identity line. If it is not the case, we talk about miscalibration (see reference). By improving calibration, one can improve the performance of the model.

You can use calibrationProfile function to visualize and assess calibration.

p <- calibrationProfile(outcome = truth, score = rscore)
p$plot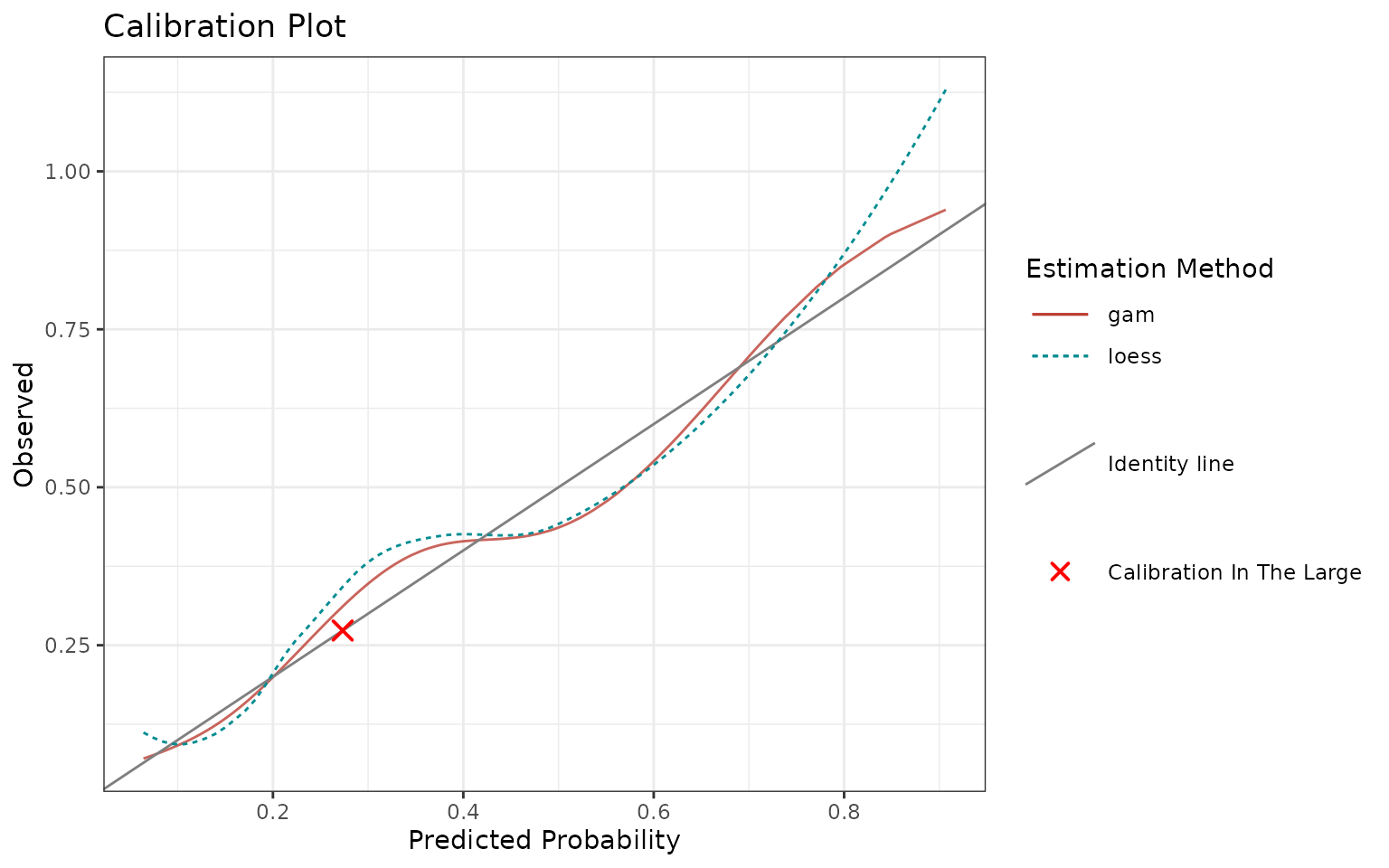

head(p$data)

## # A tibble: 6 × 5
##   method  score percentile outcome estimate
##   <chr>   <dbl>      <dbl>   <dbl>    <dbl>
## 1 gam    0.0640    0.00300       0   0.0707
## 2 gam    0.0654    0.00601       0   0.0714
## 3 gam    0.0659    0.00901       1   0.0716
## 4 gam    0.0702    0.0120        0   0.0739
## 5 gam    0.0709    0.0150        0   0.0742
## 6 gam    0.0721    0.0180        1   0.0749

There is an extensive documentation of this function with examples if you run ?calibrationProfile.

To briefly highlight the functionalities:

• Use the methods argument to specify the desired estimation method (see the last section). In this case, "asis" is not allowed.

• Use include argument to specify what additional quantities to show:

  • "loess": Adds non-parametric Loess fit.

  • "citl": Adds “Calibration in the Large”, an overall mean of outcome and score.

  • "rug": Adds “rug”, i.e. ticks on x-axis showing the individual data points (top axis shows score for outcome == 1, bottom axis shows score for outcome == 0).

  • "datapoints": Similar to rug, just shows jittered points instead of ticks.

• plot.raw sets whether to plot raw values or percentiles.

• rev.order sets whether to reverse the order of the score (useful if higher score refers to lower outcome).

• Use margin.type to add a marginal plot through ggExtra::ggMarginal. You can select one of c("density", "histogram", "boxplot", "violin", "densigram"). It adds the selected 1d graph on top of the calibrtion plot and is suitable for investigating the score.

• The output is the plot itself and the underlying data.

Sensitivity and specificity

Ultimately, we provide a sensitivity and specificity plot. For these quantities you need to define a cutoff with which you can trasnform the numeric score to binary. We use data-driven cutoffs, meaning that every single value of score is taken as the cutoff, allowing us to visualize the sensitivity and specificity as a function of score. This graph may inform you of the best suitable cutoff for your model, although we usually recommend to output the whole score range, not just the binary decisions.

You can use sensSpec function to visualize and assess sensitivity and specificity.

p <- sensSpec(outcome = truth, score = rscore)
p$plot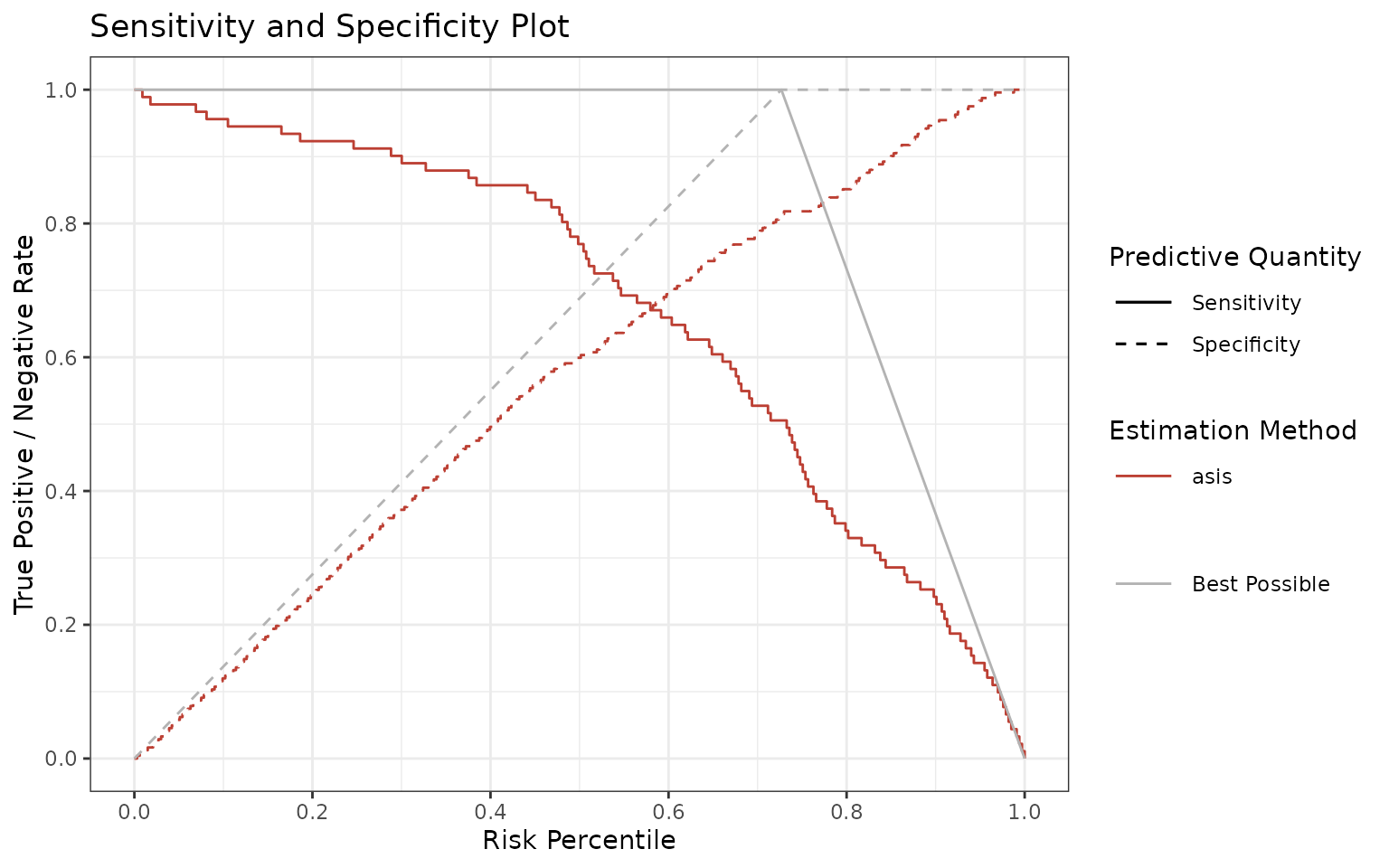

head(p$data)

## # A tibble: 6 × 5
##   method  score percentile pf            value
##   <chr>   <dbl>      <dbl> <chr>         <dbl>
## 1 asis   0.0640    0       Sensitivity 1      
## 2 asis   0.0640    0       Specificity 0      
## 3 asis   0.0640    0.00300 Sensitivity 1      
## 4 asis   0.0640    0.00300 Specificity 0.00413
## 5 asis   0.0654    0.00601 Sensitivity 1      
## 6 asis   0.0654    0.00601 Specificity 0.00826

There is an extensive documentation of this function with examples if you run ?sensSpec.

To briefly highlight the functionalities:

• Use the methods argument to specify the desired estimation method (see the last section) or use "asis" for no estimation.

• show.best controls whether to show/hide the theoretically best possible sensitivity and specificity.

• plot.raw sets whether to plot raw values or percentiles.

• rev.order sets whether to reverse the order of the score (useful if higher score refers to lower outcome).

Adjusting the graphs

All the functions return the ggplot object under the $plot element so you can further adjust it by adding more layers. There is a risk that you might overwrite one of the previous layers, so please double check your results.

For example, if you want to use the following graph

p <- riskProfile(
  outcome = truth, 
  score = rscore, 
  methods = c("asis", "gam"), 
  include = "PC"
)
p$plot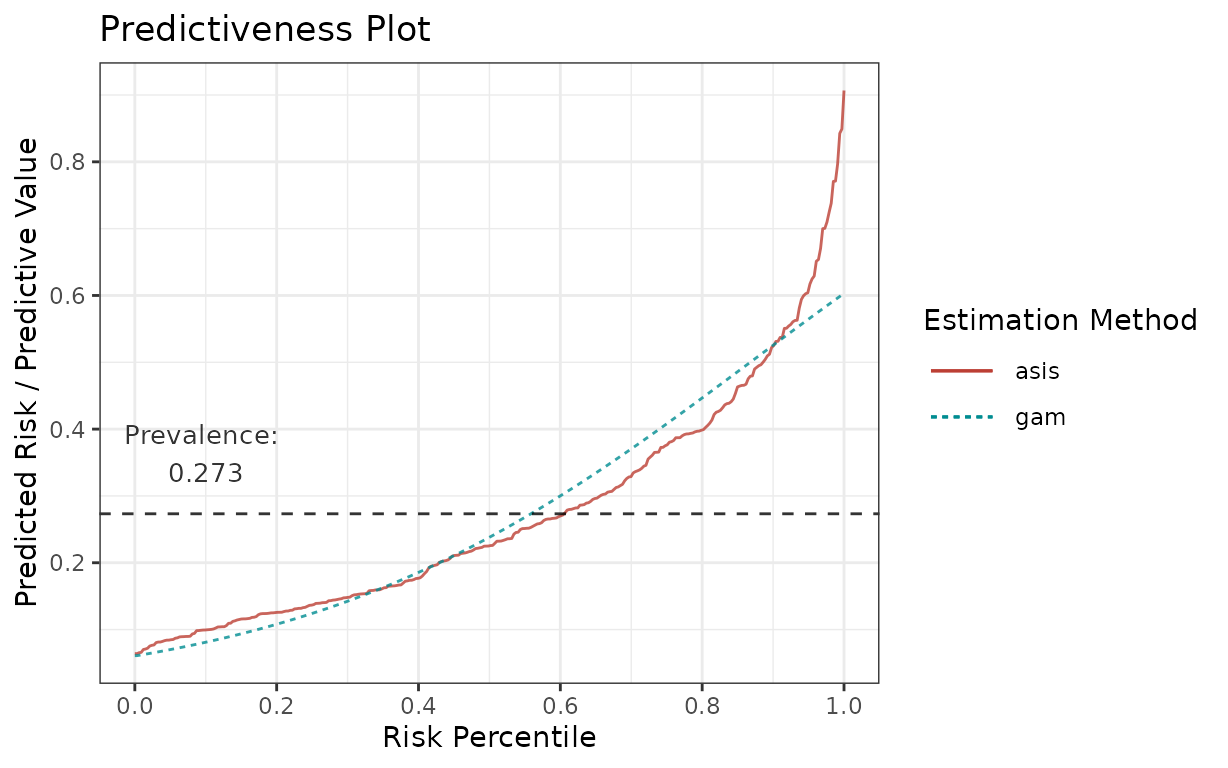

for your publication with some minor adjustments, here is how you can change colours and line types:

library(ggplot2)
p$plot + 
  # change the colours to blue for "gam" and darkgreen for "asis"
  scale_colour_manual(values = c("gam" = "blue", "asis" = "darkgreen")) + 
  # change the linetypes to solid for both
  scale_linetype_manual(values = c("gam" = "solid", "asis" = "solid"))

## Scale for colour is already present.
## Adding another scale for colour, which will replace the existing scale.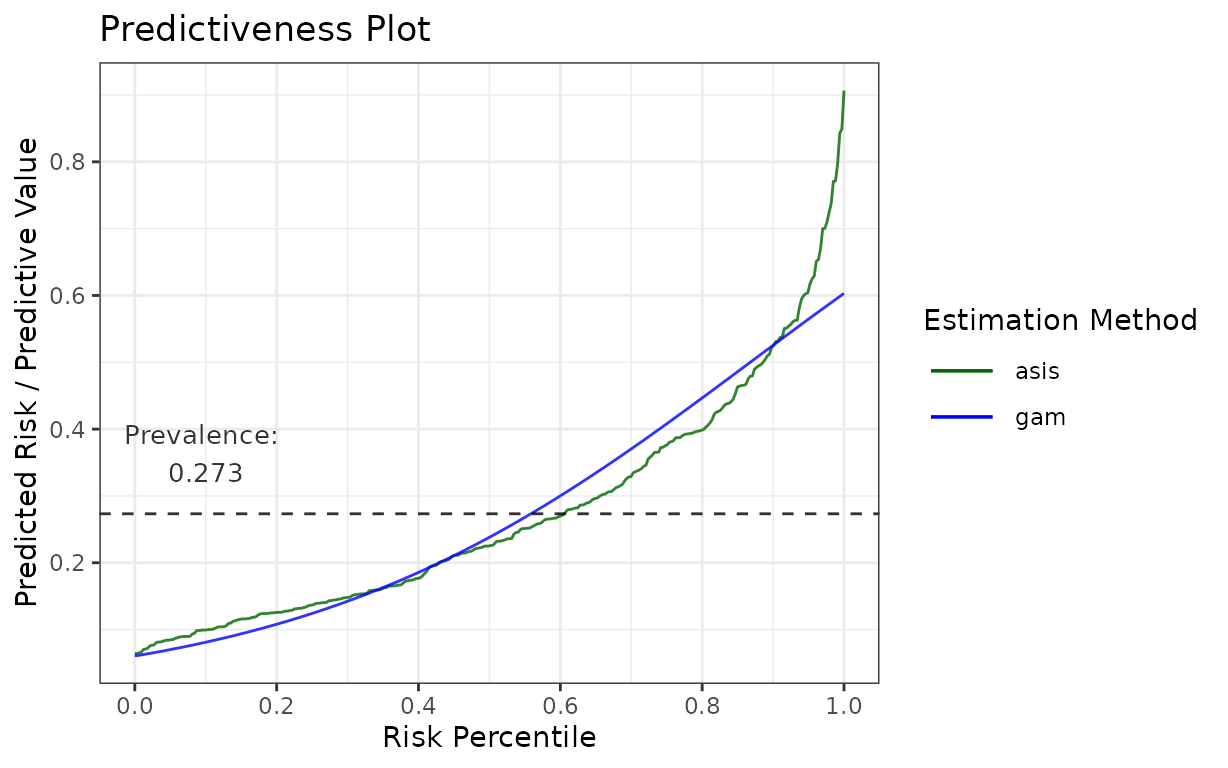

Otherwise, you can use the $data element to construct your own graph as well.

Estimations in stats4phc

For all the plotting functions from this package, there is a possibility to define an estimation function, which will be applied on the given score. In calibrationProfile, this serves as a calibration curve. In riskProfile, this smooths the given score. All of this is always driven by the methods argument, which is available in each of the plotting functions.

There are couple of predefined estimation methods:

## [1] "asis"    "binned"  "cgam"    "gam"     "mspline" "pava"

Users can also define their own estimation function if needed.

Predefined estimation functions

The predefined estimation functions can be given as a character, in which case the default values of the estimation function arguments will be used, or as a list, in which case you can change the parameters of the estimation.

The character vector approach, using the default parameter values, is as follows:

methods = c("gam", "cgam")

To see the possible arguments and their defaults, look into the estimation function documentation, which is always available as getXest, where X stands for the estimation function (e.g. getCGAMest). Here is the list of all:

## [1] "getASISest"    "getBINNEDest"  "getCGAMest"    "getGAMest"    
## [5] "getMSPLINEest" "getPAVAest"

For example, by running ?getGAMest, we see that "gam" sets k, the number of knots, to -1, which refers to automatic selection.

Otherwise, you can specify the estimation methods as a list, in which case you can change the argument values, e.g.:

methods = list(
  gam3 = list(method = "gam", k = 3),
  gam5 = list(method = "gam", k = 5),
  cgam = list(method = "cgam", numknots = 0) # automatic knot selection
)

Note that all the list elements must be (uniquely) named, both inner and outer lists, and there always needs to be an element "method", which specifies the estimation function.

By default, "gam", "cgam", and "mspline" always fit on percentiles. If you want to change this, you need to specify it through an argument fitonPerc, such as:

methods = list(mspline = list(method = "mspline", fitonPerc = FALSE))

Finally, method "asis" is a specific “estimation method”, which takes the input “as is”, it does not perform any estimation. It is listed here for consistency. You can use this method in case you want to assess your score without any adjustments.

User-defined estimation functions

You can also define your own estimation function. To do so, define a function which:

• takes exactly these 2 arguments: outcome and score.

• performs the estimation of your choice, based on outcome and score.

• returns a data.frame of exactly these 4 columns: score, percentile (percentile of score), outcome, and estimate (result of your estimation).

Here is an example:

# User-defined estimation function - logistic regression

# Function needs to take exactly these two arguments
my_logistic <- function(outcome, score) {
  # Calculate percentiles
  perc <- ecdf(score)(score)
  # Fit logistic regression on percentiles
  m <- glm(outcome ~ perc, family = "binomial")
  # Generate predictions
  preds <- predict(m, type = "response")
  # Return a data.frame with these 4 columns
  return(
    data.frame(
      score = score,
      percentile = perc,
      outcome = outcome,
      estimate = preds
    )
  )
}

# Then provide it to the `methods` argument as a named list
methods = list(my_logistic = my_logistic)

Note that you can also combine user-defined functions with already predefined functions, e.g.:

methods = list(my_logistic = my_logistic, gam = list(method = "gam"))

Hint: if you cannot get your function to work correctly, use browser() in your function to interactively debug it in order to see what’s wrong.