2. Conduct a hybrid control analysis on a dataset using BDB

In this vignette, you’ll learn how to conduct Bayesian dynamic borrowing (BDB) analyses using psborrow2.

Before you start

The functionality in this article relies on Stan for model fitting, specifically via the CmdStan and cmdstanr tools.

If you haven’t used CmdStan before you’ll need to install the R package and the external program. More information can be found in the cmdstanr installation guide.

The short version is:

# Install the cmdstanr package
install.packages("cmdstanr", repos = c("https://stan-dev.r-universe.dev", getOption("repos")))
library(cmdstanr)

# Install the external CmdStan program
check_cmdstan_toolchain()
install_cmdstan(cores = 2)

Now you’re ready to start with psborrow2.

library(psborrow2)
library(cmdstanr)

Creating an analysis object

For a BDB analysis in psborrow2, we need to create an object of class Analysis which contains all the information needed to build a model and compile an MCMC sampler using Stan. To create an Analysis object, we will call the function create_analysis_obj(). Let’s look at the four required arguments to this function and evaluate them one-at-a-time.

create_analysis_obj(
  data_matrix,
  outcome,
  borrowing,
  treatment
)

1. `data_matrix`

Required elements

data_matrix is where we input the one-row-per-patient numeric matrix for our analysis. The column names of the matrix are not fixed, so the names of columns will be specified in the outcome, treatment, and borrowing sections.

There are two columns required for all analyses:

A flag denoting receipt of the experimental intervention (1) or not (0)
A flag denoting whether the patient was part of the external data source (1) or the internal trial (0)

Time-to-event

If the outcome is time-to-event, then two additional columns are needed:

The duration of follow-up for each patient
A flag denoting whether the patient was censored (1) or not (0)

Binary endpoints

If the outcome is binary, one additional column is needed:

A flag denoting whether a patient had the event of interest (1) or not (0)

Covariates

Covariates may also be included in BDB analyses. These should be included in the data matrix if the plan is to adjust for them.

Note Only numeric matrices are supported. See Example data for creating such a matrix from a data.frame.

Note No missing data is currently allowed, all values must be non-missing.

Example data

We will be using an example dataset stored in psborrow2 (example_matrix). If you are starting from a data frame or tibble, you can easily create a suitable matrix with the psborrow2 helper function create_data_matrix().

Creating a data matrix with `create_data_matrix()`

# Start with data.frame
diabetic_df <- survival::diabetic

# For demonstration purposes, let some patients be external controls
diabetic_df$external <- ifelse(diabetic_df$trt == 0 & diabetic_df$id > 1000, 1, 0)

# Create the censor flag
diabetic_df$cens <- ifelse(diabetic_df$status == 0, 1, 0)

diabetes_matrix <- create_data_matrix(
  diabetic_df,
  outcome = c("time", "cens"),
  trt_flag_col = "trt",
  ext_flag_col = "external",
  covariates = ~ age + laser + risk
)
# Call `add_covariates()` with `covariates =  c("age", "laserargon", "risk") `

head(diabetes_matrix)
#    time cens trt external age laserargon risk
# 1 46.23    1   0        0  28          1    9
# 2 46.23    1   1        0  28          1    9
# 3 42.50    1   1        0  12          0    8
# 4 31.30    0   0        0  12          0    6
# 5 42.27    1   1        0   9          0   11
# 6 42.27    1   0        0   9          0   11

`psborrow2` example matrix

Let’s look at the first few rows of the example matrix:

head(example_matrix)
#      id ext trt cov4 cov3 cov2 cov1       time status cnsr resp
# [1,]  1   0   0    1    1    1    0  2.4226411      1    0    1
# [2,]  2   0   0    1    1    0    1 50.0000000      0    1    1
# [3,]  3   0   0    0    0    0    1  0.9674372      1    0    1
# [4,]  4   0   0    1    1    0    1 14.5774738      1    0    1
# [5,]  5   0   0    1    1    0    0 50.0000000      0    1    0
# [6,]  6   0   0    1    1    0    1 50.0000000      0    1    0

The column definitions are below:

ext, 0/1, flag for external controls
trt, 0/1, flag for treatment arm
cov1, 0/1, a baseline covariate
cov2, 0/1, a baseline covariate
time, positive numeric, survival time
cnsr, 0/1, censoring indicator
resp, 0/1, indicator for binary response outcome

2. `outcome`

psborrow2 currently supports four outcomes:

Time-to-event with exponential distribution (constant hazard), created with outcome_surv_exponential()
Time-to-event with Weibull distribution and proportional hazards parametrization, created with outcome_surv_weibull_ph()
Binary endpoints with a Bernoulli distribution and using logistic regression, created with outcome_bin_logistic()
Continuous endpoints with a normal distribution, created with outcome_cont_normal()

After we select which outcome and distribution we want, we need to specify a prior distribution for the baseline event rate, baseline_prior. In this case, baseline_prior is a log hazard rate. Let’s assume we have no prior knowledge on this event rate, so we’ll specify an uninformative prior: prior_normal(0, 1000).

For our example, let’s conduct a time-to-event analysis using the exponential distribution.

outcome <- outcome_surv_exponential(
  time_var = "time",
  cens_var = "cnsr",
  baseline_prior = prior_normal(0, 1000)
)
outcome
# Outcome object with class OutcomeSurvExponential 
# 
# Outcome variables:
# time_var cens_var 
#   "time"   "cnsr" 
# 
# Baseline prior:
# Normal Distribution
# Parameters:
#  Stan  R    Value
#  mu    mean    0 
#  sigma sd   1000

3. `borrowing`

psborrow2 supports three different borrowing methods, each of which has its own class:

No borrowing: This is the internal trial comparison without any external data. Use borrowing_none() to specify this.
Full borrowing: This is pooling of the external and internal control arms. Use borrowing_full() to specify this.
Bayesian dynamic borrowing with the hierarchical commensurate prior: This borrowing is as described in Hobbs et al. (2011) and uses the hierarchical commensurate prior. Use borrowing_hierarchical_commensurate() to specify this.

The column name for the external control column flag in our matrix is also required and passed to ext_flag_col.

Finally, for dynamic borrowing only, the hyperprior distribution on the commensurability parameter must be specified. This hyperprior determines (along with the comparability of the outcomes between internal and external controls) how much borrowing of the external control group will be performed. Example hyperpriors include largely uninformative inverse gamma distributions e.g., prior_gamma(alpha = .001, beta = .001) as well as more informative distributions e.g., prior_gamma(alpha = 1, beta = .001), though any distribution on the positive real line can be used. Distributions with more density at higher values (i.e., higher precision) will lead to more borrowing. We’ll choose an uninformative gamma prior in this example.

Note: Prior distributions are outlined in greater detail in a separate vignette, see vignette('prior_distributions', package = 'psborrow2').

borrowing <- borrowing_hierarchical_commensurate(
  ext_flag_col = "ext",
  tau_prior = prior_gamma(0.001, 0.001)
)
borrowing
# Borrowing object using the  Bayesian dynamic borrowing with the hierarchical commensurate prior  approach
# 
# External control flag: ext 
# 
# Commensurability parameter prior:
# Gamma Distribution
# Parameters:
#  Stan  R     Value
#  alpha shape 0.001
#  beta  rate  0.001
# Constraints: <lower=0>

3. `treatment`

Finally, treatment details are outlined in treatment_details(). Here, we first specify the column for the treatment flag in trt_flag_col. In addition, we need to specify the prior on the effect estimate, trt_prior. We’ll use another uninformative normal distribution for the prior on the treatment effect:

treatment <- treatment_details(
  trt_flag_col = "trt",
  trt_prior = prior_normal(0, 1000)
)
treatment
# Treatment object
# 
# Treatment flag column: trt 
# 
# Treatment effect prior:
# Normal Distribution
# Parameters:
#  Stan  R    Value
#  mu    mean    0 
#  sigma sd   1000

Application

Now that we have thought through each of the inputs to create_analysis_obj(), let’s create an analysis object:

anls_obj <- create_analysis_obj(
  data_matrix = example_matrix,
  outcome = outcome,
  borrowing = borrowing,
  treatment = treatment,
  quiet = TRUE
)

The Stan model compiled successfully and informed us that we are ready to begin sampling.

Note that if you are interested in seeing the Stan code that was generated, you can use the get_stan_code() function to see the full Stan code that will be compiled.

get_stan_code(anls_obj)
# 
#   functions {
#   
# }
# 
#   data {
#   int<lower=0> N;
#   vector[N] trt;
#   vector[N] time;
# vector[N] cens;
# 
#   matrix[N,2] Z;
#   
# }
# 
#   parameters {
# real beta_trt;
# 
# real<lower=0> tau;
# vector[2] alpha;
# 
# }
# 
#   transformed parameters {
#   real HR_trt = exp(beta_trt);
# }
# 
#   model {
#   vector[N] lp;
#   vector[N] elp;
#   beta_trt ~ normal(0, 1000);
#   lp = Z * alpha + trt * beta_trt;
# elp = exp(lp) ;
#   
#   
#   tau ~ gamma(0.001, 0.001) ;
# real sigma;
# sigma = 1 / tau;
# alpha[2] ~ normal(0, 1000) ;
# alpha[1] ~ normal(alpha[2], sqrt(sigma)) ;
#   for (i in 1:N) {
#    if (cens[i] == 1) {
#       target += exponential_lccdf(time[i] | elp[i] );
#    } else {
#       target += exponential_lpdf(time[i] | elp[i] );
#    }
# }
# }

Sampling from an analysis object

We can take draws from the posterior distribution using the function mcmc_sample(). This function takes as input our Analysis object and any arguments (other than the data argument) that are passed to CmdStanModel objects. Note that running this may take a few minutes.

results <- mcmc_sample(anls_obj,
  iter_warmup = 2000,
  iter_sampling = 50000,
  chains = 4,
  seed = 112233
)

Summarizing results

As a CmdStanMCMC object, results has several methods which are outlined on the cmdstanr website. For instance, we can see a see a summary of the posterior distribution samples with results$summary():

results$summary()
# # A tibble: 6 × 10
#   variable      mean    median     sd    mad          q5      q95  rhat ess_bulk
#   <chr>        <dbl>     <dbl>  <dbl>  <dbl>       <dbl>    <dbl> <dbl>    <dbl>
# 1 lp__     -1618.    -1618.    1.50   1.29   -1621.      -1.62e+3  1.00   71314.
# 2 beta_trt    -0.155    -0.158 0.199  0.198     -0.477    1.74e-1  1.00   85216.
# 3 tau          1.21      0.506 1.92   0.693      0.00418  4.74e+0  1.00   81024.
# 4 alpha[1]    -3.36     -3.35  0.161  0.161     -3.63    -3.10e+0  1.00   86029.
# 5 alpha[2]    -2.40     -2.40  0.0557 0.0557    -2.49    -2.31e+0  1.00  132062.
# 6 HR_trt       0.873     0.854 0.176  0.168      0.620    1.19e+0  1.00   85216.
# # ℹ 1 more variable: ess_tail <dbl>

The summary includes information for several parameter estimates from our BDB model. Because it may not be immediately clear what the parameters from the Stan model refer to, psborrow2 has a function which returns a variable dictionary from the analysis object to help interpret these parameters:

variable_dictionary(anls_obj)
#   Stan_variable                        Description
# 1           tau         commensurability parameter
# 2      alpha[1] baseline log hazard rate, internal
# 3      alpha[2] baseline log hazard rate, external
# 4      beta_trt                   treatment log HR
# 5        HR_trt                       treatment HR

We can also capture all of the draws by calling results$draws(), which returns an object of class draws. draws objects are common in many MCMC sampling software packages and allow us to leverage packages such as posterior and bayesplot.

draws <- results$draws()
print(draws)
# # A draws_array: 50000 iterations, 4 chains, and 6 variables
# , , variable = lp__
# 
#          chain
# iteration     1     2     3     4
#         1 -1616 -1616 -1616 -1616
#         2 -1616 -1616 -1618 -1618
#         3 -1616 -1617 -1619 -1617
#         4 -1616 -1618 -1619 -1618
#         5 -1617 -1617 -1617 -1617
# 
# , , variable = beta_trt
# 
#          chain
# iteration     1      2      3      4
#         1 -0.20 -0.009 -0.022 -0.109
#         2 -0.31 -0.092 -0.167 -0.305
#         3 -0.16 -0.082  0.027  0.092
#         4 -0.24 -0.319 -0.092  0.226
#         5 -0.30 -0.081 -0.012 -0.439
# 
# , , variable = tau
# 
#          chain
# iteration    1    2    3    4
#         1 1.62 1.14 1.94 2.58
#         2 0.84 1.03 1.32 0.23
#         3 0.48 1.90 0.61 1.12
#         4 1.46 0.48 0.18 0.48
#         5 0.33 1.64 0.32 2.15
# 
# , , variable = alpha[1]
# 
#          chain
# iteration    1    2    3    4
#         1 -3.4 -3.4 -3.5 -3.4
#         2 -3.3 -3.4 -3.5 -3.4
#         3 -3.4 -3.4 -3.7 -3.5
#         4 -3.3 -3.4 -3.6 -3.6
#         5 -3.3 -3.5 -3.5 -3.2
# 
# # ... with 49995 more iterations, and 2 more variables

psborrow2 also has a function to rename variables in draws objects to be more interpretable, rename_draws_covariates(). This function uses the variable_dictionary labels. Let’s use it here to make the results easier to interpret:

draws <- rename_draws_covariates(draws, anls_obj)
summary(draws)
# # A tibble: 6 × 10
#   variable          mean   median     sd    mad       q5      q95  rhat ess_bulk
#   <chr>            <dbl>    <dbl>  <dbl>  <dbl>    <dbl>    <dbl> <dbl>    <dbl>
# 1 lp__          -1.62e+3 -1.62e+3 1.50   1.29   -1.62e+3 -1.62e+3  1.00   71314.
# 2 treatment lo… -1.55e-1 -1.58e-1 0.199  0.198  -4.77e-1  1.74e-1  1.00   85216.
# 3 commensurabi…  1.21e+0  5.06e-1 1.92   0.693   4.18e-3  4.74e+0  1.00   81024.
# 4 baseline log… -3.36e+0 -3.35e+0 0.161  0.161  -3.63e+0 -3.10e+0  1.00   86029.
# 5 baseline log… -2.40e+0 -2.40e+0 0.0557 0.0557 -2.49e+0 -2.31e+0  1.00  132062.
# 6 treatment HR   8.73e-1  8.54e-1 0.176  0.168   6.20e-1  1.19e+0  1.00   85216.
# # ℹ 1 more variable: ess_tail <dbl>

Using `bayesplot`

With draws objects and the bayesplot package, we can create many useful visual summary plots. We can visualize the marginal posterior distribution of a variable we are interested in by plotting histograms of the draws with the function mcmc_hist(). Let’s do that for the Hazard ratio for the treatment effect and for our commensurability parameter, tau.

bayesplot::mcmc_hist(draws, c("treatment HR", "commensurability parameter"))

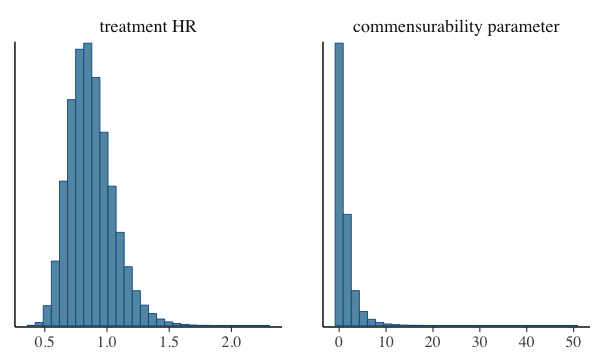
plot of chunk mcmc-hist

We can see other plots that help us understand and diagnose problems with the MCMC sampler, such as trace and rank plots:

bayesplot::color_scheme_set("mix-blue-pink")

bayesplot::mcmc_trace(
  draws[1:5000, 1:2, ], # Using a subset of draws only
  pars = c("treatment HR", "commensurability parameter"),
  n_warmup = 1000
)

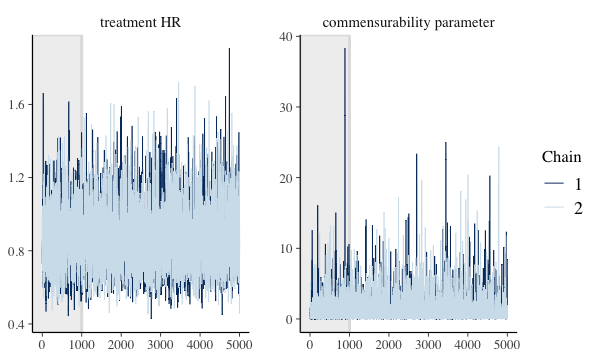
plot of chunk mcmc-trace

Many other functions are outlined in the bayesplot vignettes.

Using `posterior`

draws objects are also supported by the posterior package, which provides many other tools for analyzing MCMC draw data. For instance, we can use the summarize_draws() function to derive 80% credible intervals for all parameters:

library(posterior)
summarize_draws(draws, ~ quantile(.x, probs = c(0.1, 0.9)))
# # A tibble: 6 × 3
#   variable                                `10%`     `90%`
#   <chr>                                   <dbl>     <dbl>
# 1 lp__                               -1620.     -1616.   
# 2 treatment log HR                      -0.408      0.100
# 3 commensurability parameter             0.0172     3.22 
# 4 baseline log hazard rate, internal    -3.57      -3.15 
# 5 baseline log hazard rate, external    -2.47      -2.33 
# 6 treatment HR                           0.665      1.11

Another useful application of the posterior package is the evaluation of the Monte Carlo standard error for quantiles of a variable of interest:

vm <- extract_variable_matrix(draws, "treatment HR")
mcse_quantile(x = vm, probs = c(0.1, 0.5, 0.9))
#  mcse_q10  mcse_q50  mcse_q90 
# 0.0006465 0.0006845 0.0012300

posterior contains many other helpful functions, as outlined in their vignettes.

Matt Secrest and Isaac Gravestock

Before you start

Creating an analysis object

1. data_matrix

Required elements

Time-to-event

Binary endpoints

Covariates

Example data

Creating a data matrix with create_data_matrix()

psborrow2 example matrix

2. outcome

3. borrowing

3. treatment