3  Model diagnostics and performance evaluation

This page showcase the model diagnosis and performance evaluation on the ER model for binary endpoint.

Show the code 
library(tidyverse)
library(BayesERtools)
library(here)
library(posterior)
library(tidybayes)
library(bayesplot)
library(gt)

theme_set(theme_bw(base_size = 12))

3.1 Load data

Show the code 
data(d_sim_binom_cov)

d_sim_binom_cov_2 <-
  d_sim_binom_cov |>
  mutate(
    AUCss_1000 = AUCss / 1000, BAGE_10 = BAGE / 10,
    BWT_10 = BWT / 10, BHBA1C_5 = BHBA1C / 5,
    Dose = glue::glue("{Dose_mg} mg")
  )

# Grade 2+ hypoglycemia
df_er_ae_hgly2 <- d_sim_binom_cov_2 |> filter(AETYPE == "hgly2")
# Grade 2+ diarrhea
df_er_ae_dr2 <- d_sim_binom_cov_2 |> filter(AETYPE == "dr2")

var_resp <- "AEFLAG"
var_exposure <- "AUCss_1000"

3.2 Fit models

There is clear trend of E-R for hyperglycemia (95% CI doesn’t include 0) while the evidence of E-R is not seen for diarrhea (95% CI includes 0).

Show the code 
set.seed(1234)
ermod_bin_hgly2 <- dev_ermod_bin(
  data = df_er_ae_hgly2,
  var_resp = var_resp,
  var_exposure = var_exposure
)
plot_er_gof(ermod_bin_hgly2, var_group = "Dose", show_coef_exp = TRUE)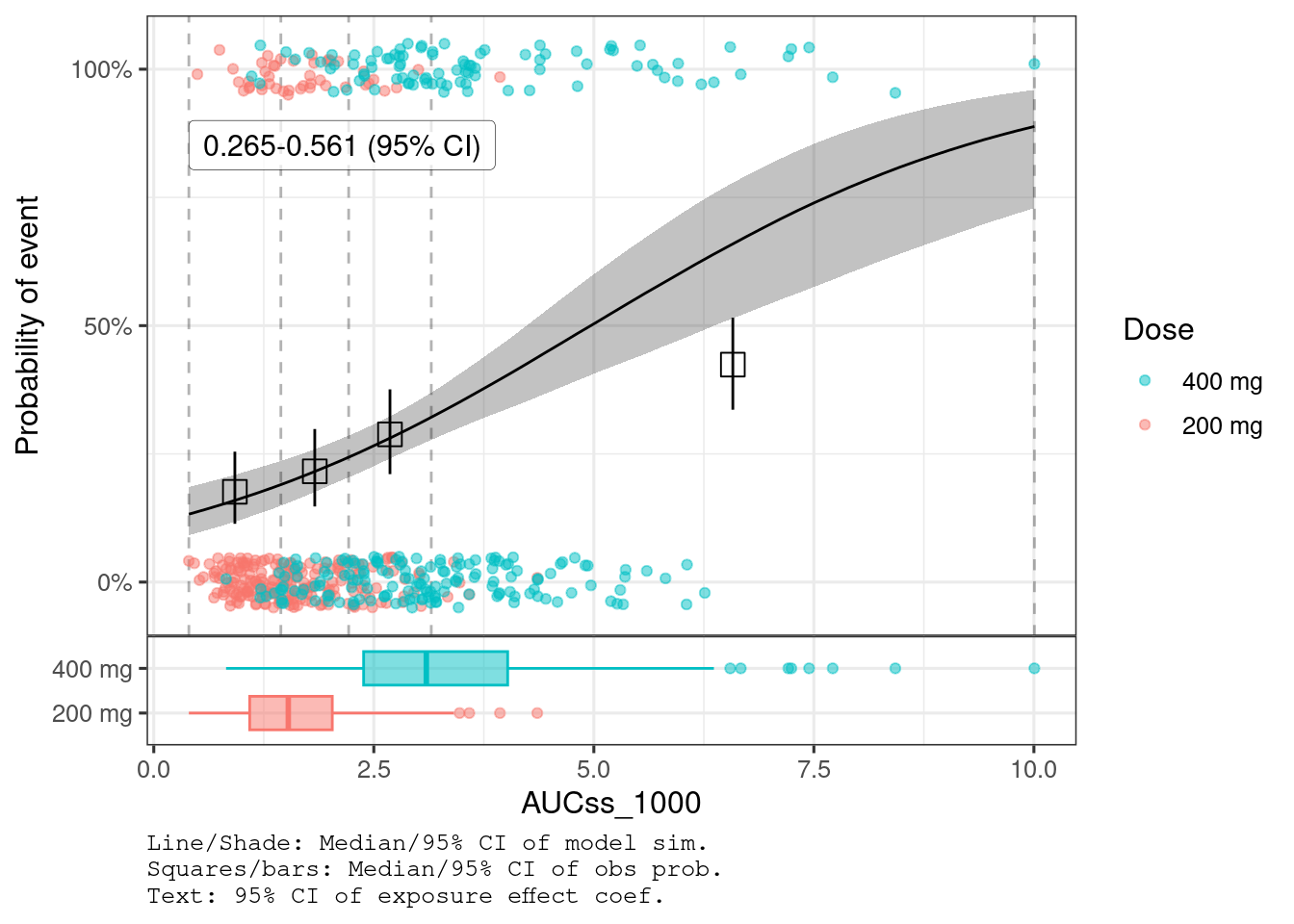
Figure 3.1
Show the code 
set.seed(1234)
ermod_bin_dr2 <- dev_ermod_bin(
  data = df_er_ae_dr2,
  var_resp = var_resp,
  var_exposure = var_exposure
)
plot_er_gof(ermod_bin_dr2, var_group = "Dose", show_coef_exp = TRUE)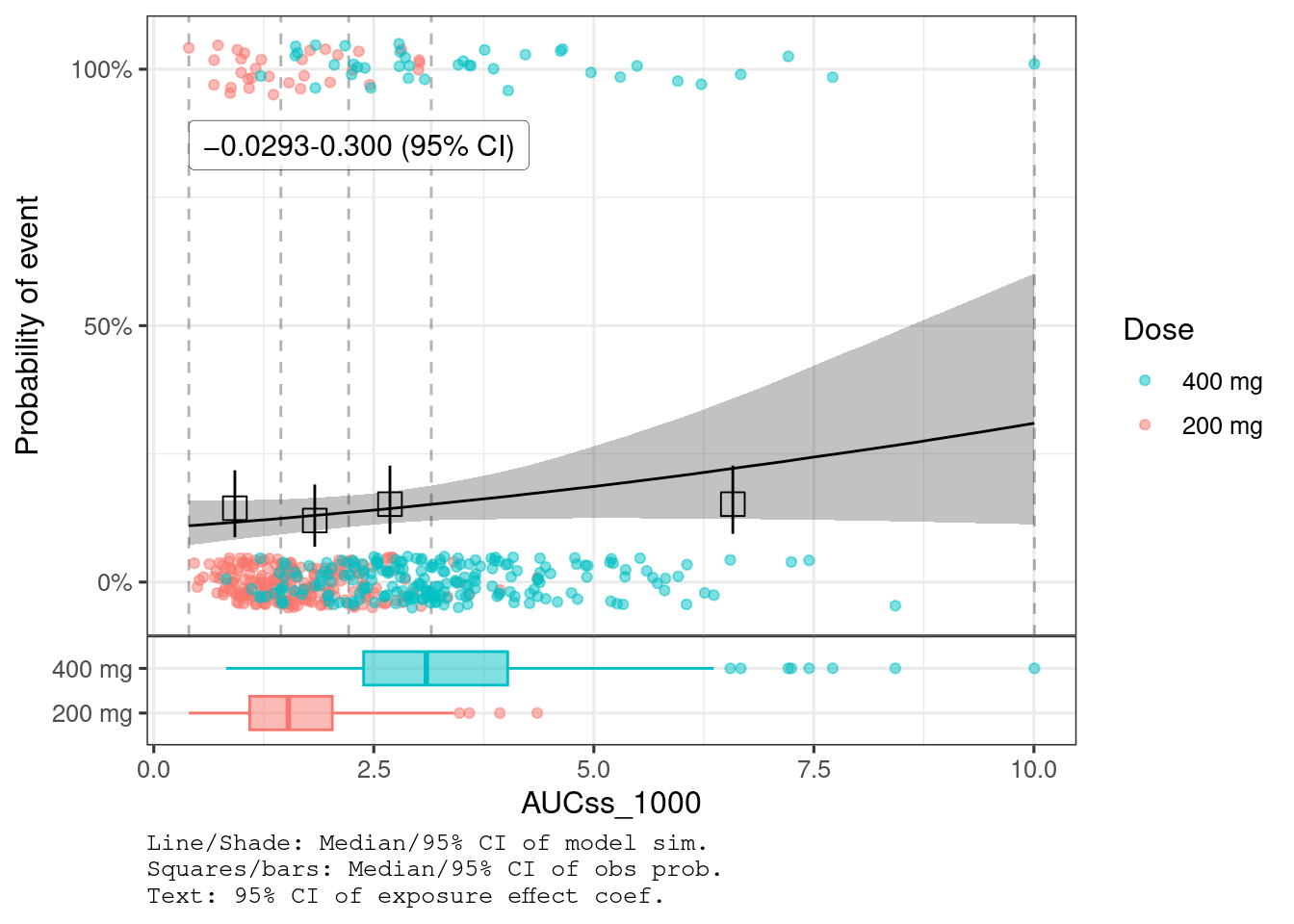
Figure 3.2

3.3 Parameter summary

You can see that AUCss effect is much stronger for hyperglycemia than diarrhea.

Show the code 
ermod_bin_hgly2 |>
  summarize_draws(mean, median, sd, ~ quantile2(.x, probs = c(0.025, 0.975)),
    default_convergence_measures()) |>
  gt() |>
  fmt_number(n_sigfig = 3)

```{=html}









variable
mean
median
sd
q2.5
q97.5
rhat
ess_bulk
ess_tail






(Intercept)
−2.05
−2.04
0.234
−2.51
−1.59
1.00
2,230
1,870




AUCss_1000
0.412
0.412
0.0761
0.265
0.561
1.00
2,150
2,140








```
Show the code 
ermod_bin_dr2 |>
  summarize_draws(mean, median, sd, ~ quantile2(.x, probs = c(0.025, 0.975)),
    default_convergence_measures()) |>
  gt() |>
  fmt_number(n_sigfig = 3)

```{=html}









variable
mean
median
sd
q2.5
q97.5
rhat
ess_bulk
ess_tail






(Intercept)
−2.15
−2.15
0.255
−2.65
−1.67
1.00
2,830
2,320




AUCss_1000
0.135
0.134
0.0832
−0.0293
0.300
1.00
2,810
2,570








```

3.4 Predictive performance evaluation

We can calculate predictive performance metrics such as AUC-ROC with eval_ermod() function. Options for evaluation data are:

  • eval_type = "training": training data
  • eval_type = "test": test data (supply to newdata argument)
  • eval_type = "kfold": k-fold cross-validation
Show the code 
metrics_hgly2_train <- eval_ermod(ermod_bin_hgly2, eval_type = "training")
metrics_hgly2_kfold <- eval_ermod(ermod_bin_hgly2, eval_type = "kfold")
Show the code 
metrics_hgly2_train |>
  gt() |>
  fmt_number(n_sigfig = 3)

```{=html}









.metric
.estimator
.estimate






roc_auc
binary
0.650




mn_log_loss
binary
0.555








```
Show the code 
metrics_hgly2_kfold |>
  gt() |>
  fmt_number(n_sigfig = 3) |>
  fmt_integer(columns = c("fold_id"))

```{=html}









fold_id
.metric
.estimator
.estimate






1
roc_auc
binary
0.631




2
roc_auc
binary
0.607




3
roc_auc
binary
0.684




4
roc_auc
binary
0.670




5
roc_auc
binary
0.663




1
mn_log_loss
binary
0.602




2
mn_log_loss
binary
0.572




3
mn_log_loss
binary
0.534




4
mn_log_loss
binary
0.581




5
mn_log_loss
binary
0.500








```

3.5 Probability of direction

Although credible intervals are preferred, there is a concept called the probability of direction which is somewhat similar to the p-value, in which the probability of the effect being far from NULL (usually set to 0) is calculated.

See ?p_direction and vignette for detail.

The exposure effect is so clear that none of the MCMC sample is below 0, leading to a “p-value” of 0. Since there were 4000 MCMC samples (nrow(as_draws_df(ermod_bin_hgly2))), it is expected that the p-value is less than 1/4000 * 2, i.e. < 0.0005 (multiplication with 2 corresponds to two-sided test).

Show the code 
bayestestR::p_direction(ermod_bin_hgly2, as_p = TRUE, as_num = TRUE)
[1] 0
Show the code 
1 / length(as_draws(ermod_bin_hgly2)$AUCss_1000) * 2
[1] 5e-04
Show the code 
bayestestR::p_direction(ermod_bin_dr2, as_p = TRUE, as_num = TRUE)
[1] 0.108
Show the code 
# Below is a direct calculation of this value
mean(as_draws(ermod_bin_dr2)$AUCss_1000 < 0) * 2
[1] 0.108

3.6 Diagnostic plots

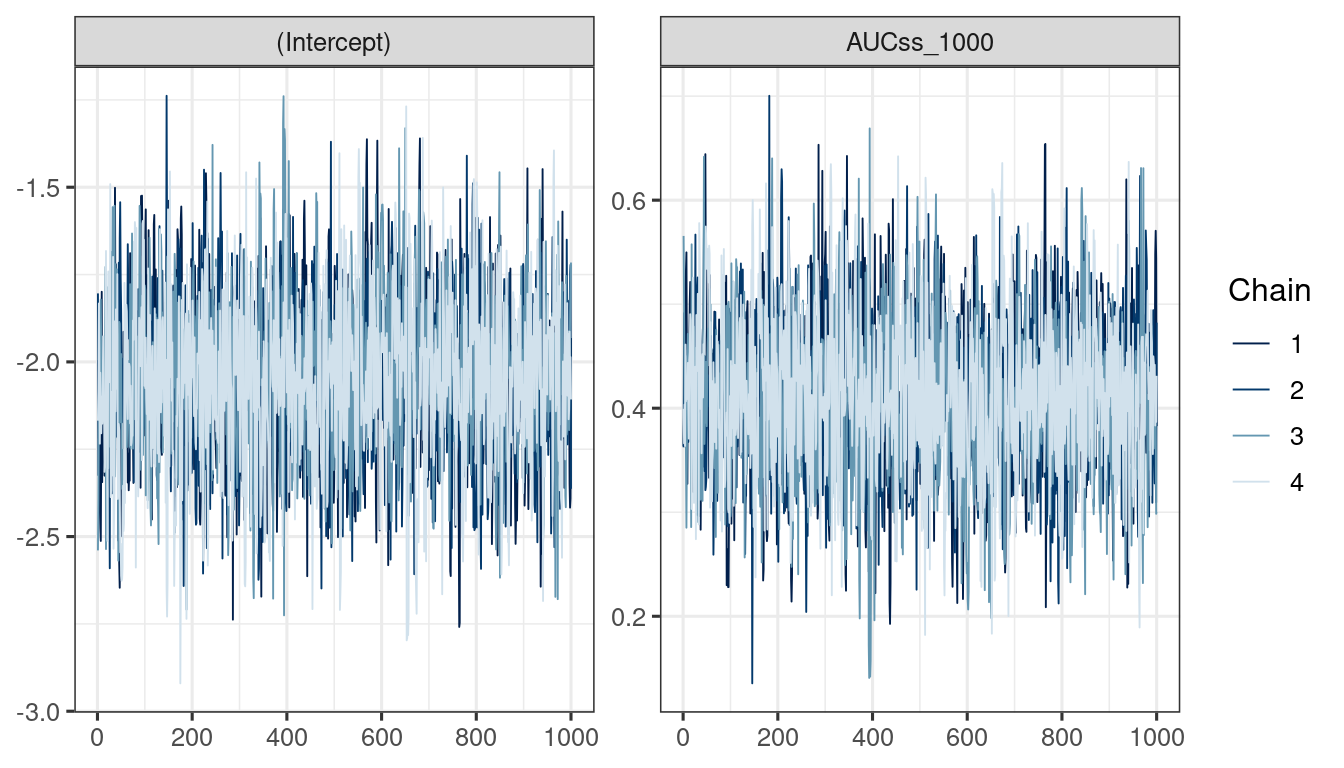
We use the bayesplot package (Cheat sheet) to visualize the model fit.

3.6.1 Convergence

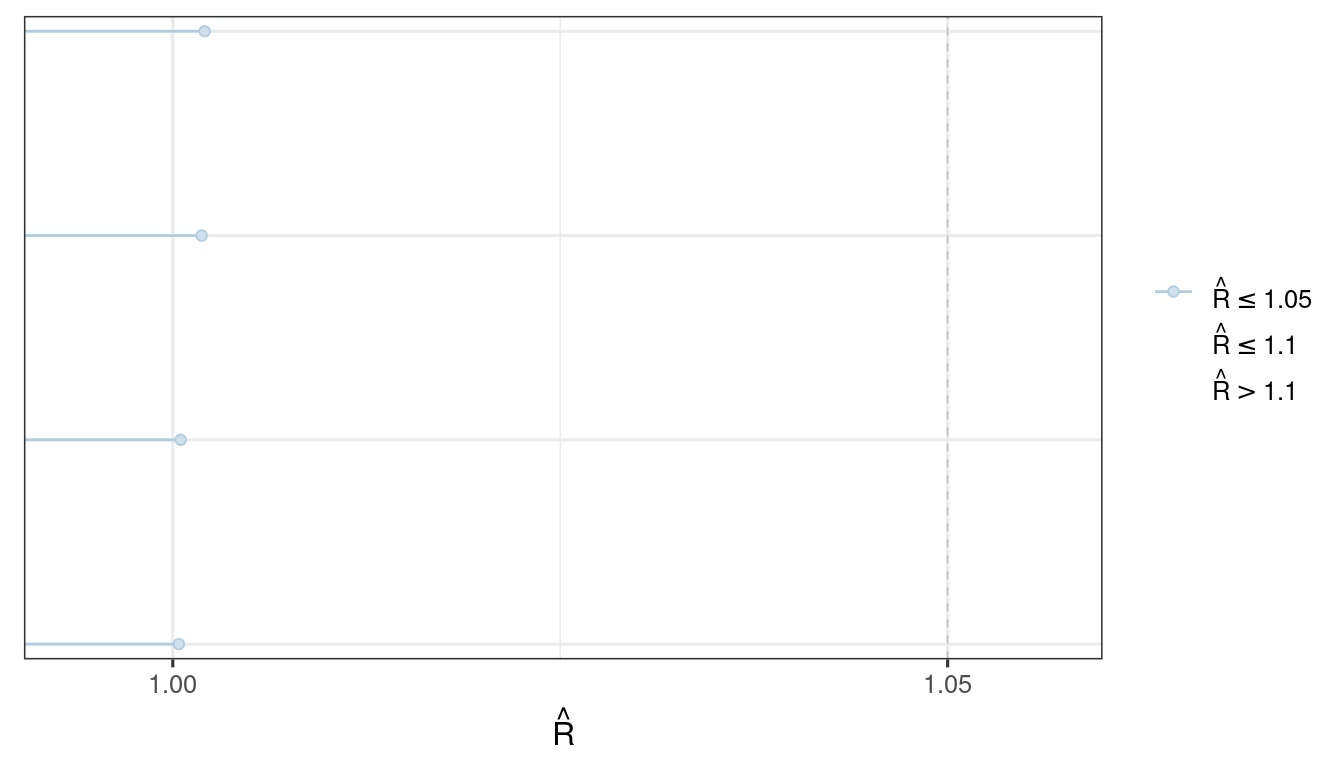
Good fit results in:

  • Parameter distributions from MCMC chains should overlap
  • Trace plots should not show any trend
  • Rhat close to 1 (e.g. < 1.1)
Show the code 
d_draws_bin_hgly2 <- as_draws_df(ermod_bin_hgly2)
mcmc_dens_overlay(d_draws_bin_hgly2)
mcmc_trace(d_draws_bin_hgly2)
mcmc_rhat(rhat(ermod_bin_hgly2$mod$stanfit))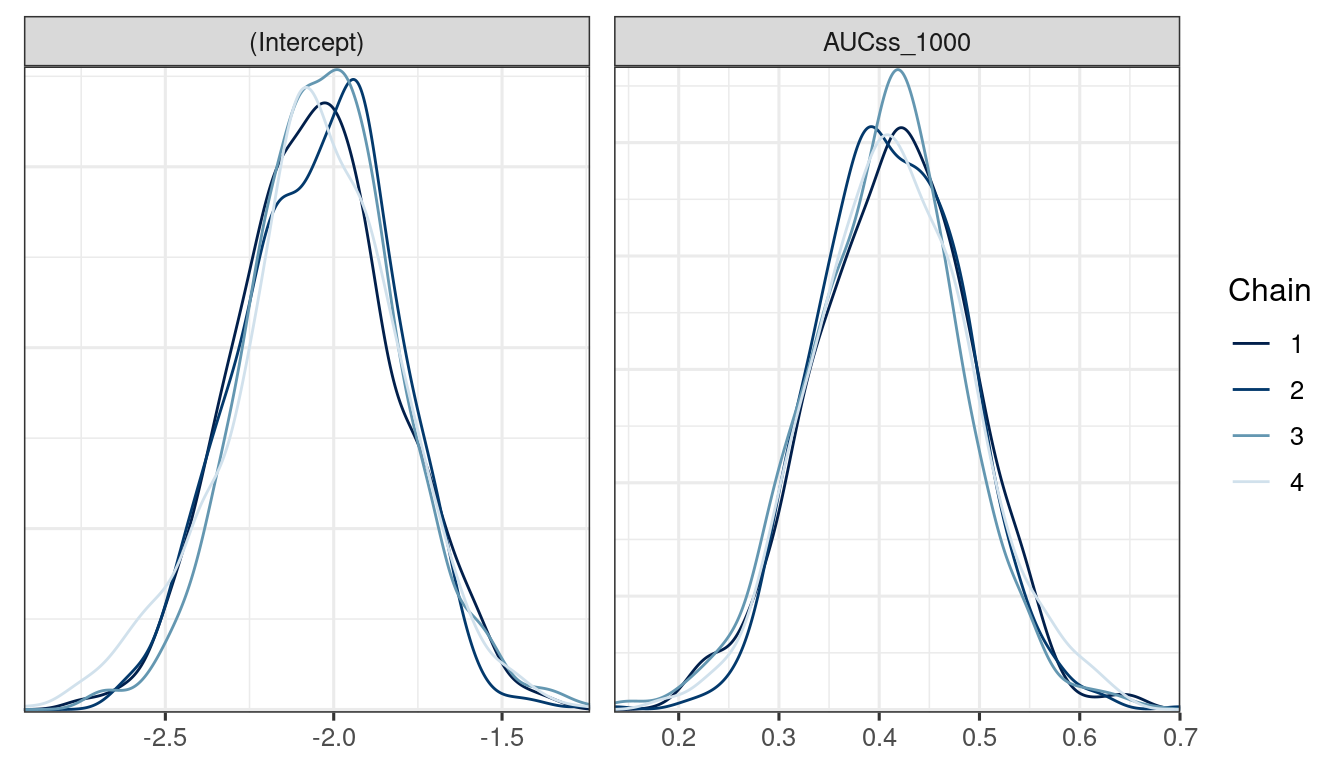
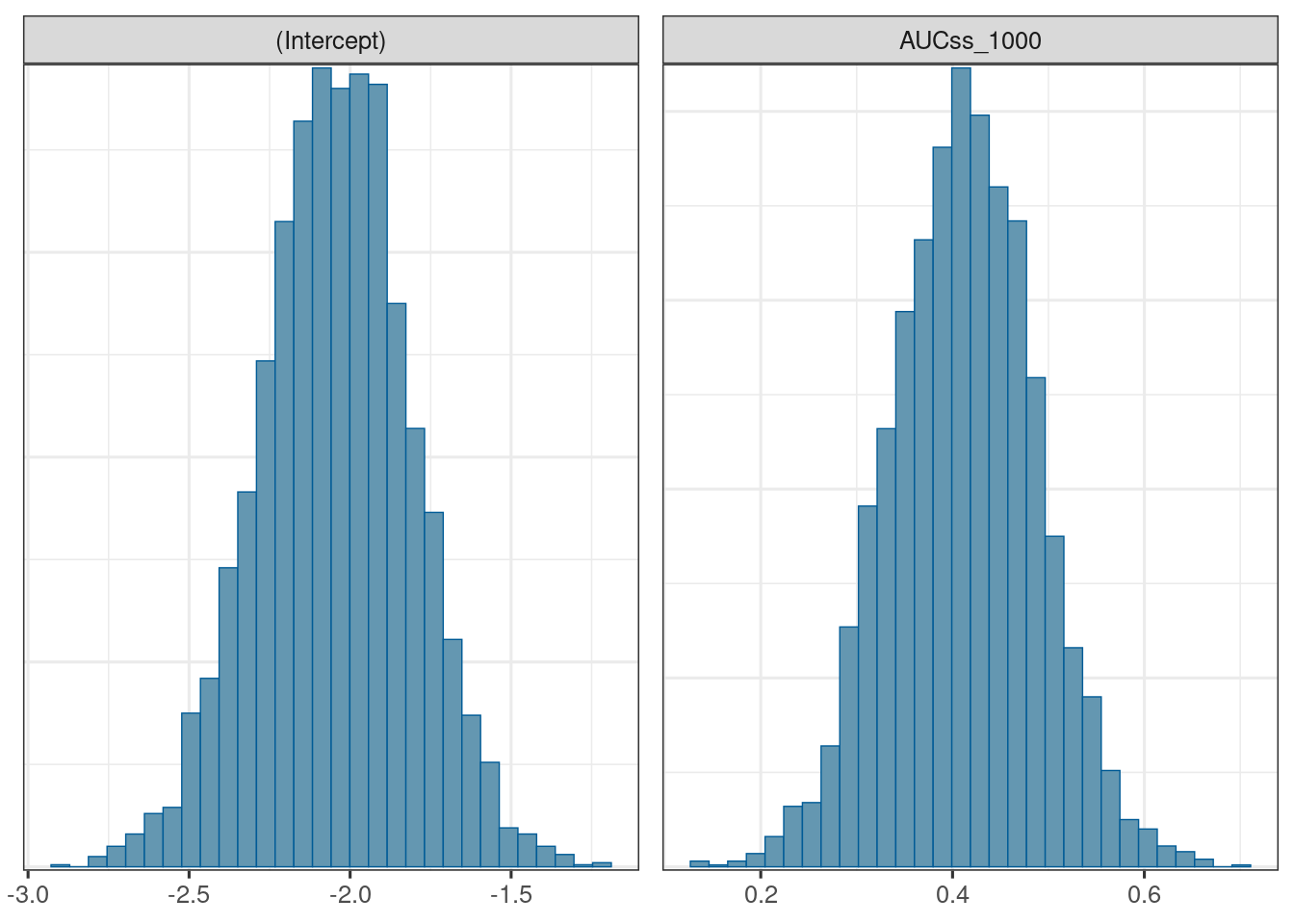
Figure 3.3
Figure 3.4
Figure 3.5

3.6.2 Parameter estimates distribution

Show the code 
mcmc_hist(d_draws_bin_hgly2)
`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
Figure 3.6
Show the code 
mcmc_pairs(d_draws_bin_hgly2,
  off_diag_args = list(size = 0.5, alpha = 0.25))
Figure 3.7