Show the code
library(tidyverse)
library(BayesERtools)
library(posterior)
library(tidybayes)
library(bayesplot)
library(loo)
library(here)
library(gt)
theme_set(theme_bw(base_size = 12))9 Simulation from fitted model
This page showcase the model simulation using the Emax model with no covariate.
9.1 Load data
Show the code
d_sim_emax# A tibble: 300 × 9
dose exposure response_1 response_2 cnt_a cnt_b cnt_c bin_d bin_e
9.2 Fit models
Show the code
set.seed(1234)
ermod_sigemax <- dev_ermod_emax(
data = d_sim_emax,
var_resp = "response_1",
var_exposure = "exposure",
gamma_fix = NULL
)
ermod_sigemax
── Emax model ──────────────────────────────────────────────────────────────────
ℹ Use `plot_er()` to visualize ER curve
── Developed model ──
---- Emax model fit with rstanemax ----
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff
emax 11.59 0.31 5.89 4.82 7.34 10.10 14.24 27.50 368.24
e0 6.68 0.20 4.08 -3.67 4.78 7.68 9.71 11.48 436.14
ec50 5254.72 193.00 4475.71 801.17 2974.18 4673.97 6385.68 15736.00 537.81
gamma 1.06 0.02 0.50 0.32 0.70 0.97 1.33 2.26 543.20
sigma 1.27 0.00 0.05 1.18 1.24 1.27 1.31 1.39 1375.87
Rhat
emax 1.01
e0 1.01
ec50 1.00
gamma 1.01
sigma 1.00
* Use `extract_stanfit()` function to extract raw stanfit object
* Use `extract_param()` function to extract posterior draws of key parameters
* Use `plot()` function to visualize model fit
* Use `posterior_predict()` or `posterior_predict_quantile()` function to get
raw predictions or make predictions on new data
* Use `extract_obs_mod_frame()` function to extract raw data
in a processed format (useful for plotting)
Another model without sigmoidal component; will be used when we do model comparison.
Show the code
set.seed(1234)
ermod_emax <- dev_ermod_emax(
data = d_sim_emax,
var_resp = "response_1",
var_exposure = "exposure",
gamma_fix = 1
)
ermod_emax
── Emax model ──────────────────────────────────────────────────────────────────
ℹ Use `plot_er()` to visualize ER curve
── Developed model ──
---- Emax model fit with rstanemax ----
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff
emax 10.11 0.07 1.71 7.93 8.98 9.72 10.81 14.42 564.00
e0 7.32 0.08 2.00 2.41 6.41 7.66 8.70 10.13 572.38
ec50 4341.84 62.80 1871.39 1704.41 3062.61 3994.85 5323.78 9061.88 887.87
gamma 1.00 NaN 0.00 1.00 1.00 1.00 1.00 1.00 NaN
sigma 1.28 0.00 0.05 1.18 1.24 1.27 1.31 1.39 1440.04
Rhat
emax 1.01
e0 1.01
ec50 1.00
gamma NaN
sigma 1.00
* Use `extract_stanfit()` function to extract raw stanfit object
* Use `extract_param()` function to extract posterior draws of key parameters
* Use `plot()` function to visualize model fit
* Use `posterior_predict()` or `posterior_predict_quantile()` function to get
raw predictions or make predictions on new data
* Use `extract_obs_mod_frame()` function to extract raw data
in a processed format (useful for plotting)
10 Extrapolation
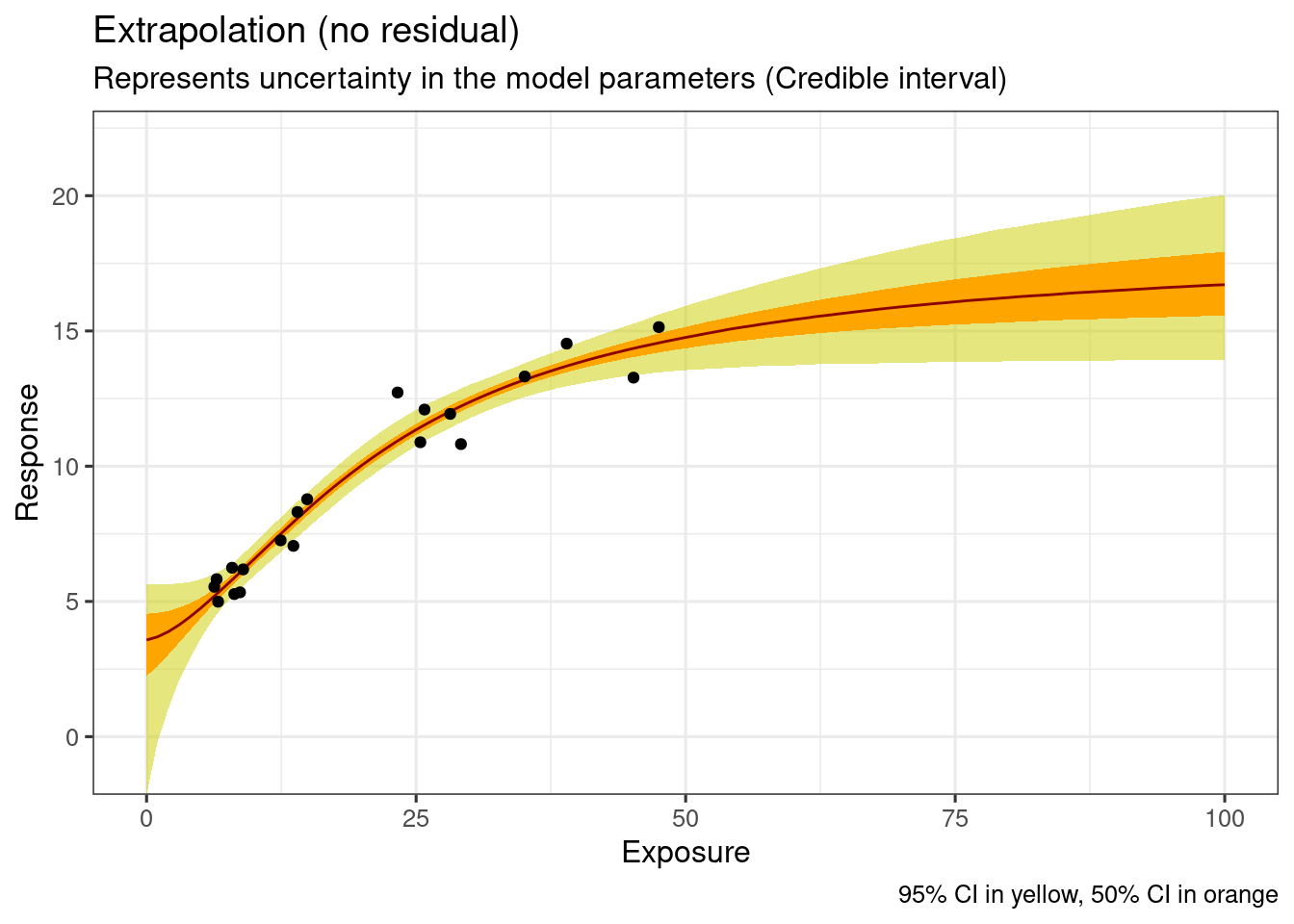
This represents uncertainty in the model parameters.
p(f(theta)|xnew, yobs)
Show the code
new_conc_vec <- seq(0, 70000, by = 500)
ersim_sigemax <-
sim_er_new_exp(ermod_sigemax, new_conc_vec)
ersim_sigemax_med_qi <-
ersim_sigemax |>
calc_ersim_med_qi(qi_width = c(0.5, 0.95))
ggplot(
data = ersim_sigemax_med_qi,
mapping = aes(x = exposure, y = .epred)
) +
geom_ribbon(
data = ersim_sigemax_med_qi |> filter(.width == 0.95),
mapping = aes(ymin = .epred.lower, ymax = .epred.upper),
fill = "yellow3",
alpha = 0.5
) +
geom_ribbon(
data = ersim_sigemax_med_qi |> filter(.width == 0.5),
mapping = aes(ymin = .epred.lower, ymax = .epred.upper),
fill = "orange1"
) +
geom_line(
data = ersim_sigemax_med_qi |> filter(.width == 0.5),
col = "darkred"
) +
geom_point(
data = d_sim_emax,
mapping = aes(y = response_1)
) +
coord_cartesian(ylim = c(5, 22)) +
labs(
x = "Exposure",
y = "Response",
title = "Extrapolation (no residual)",
subtitle = "Represents uncertainty in the model parameters (Credible interval)",
caption = "95% CI in yellow, 50% CI in orange"
)
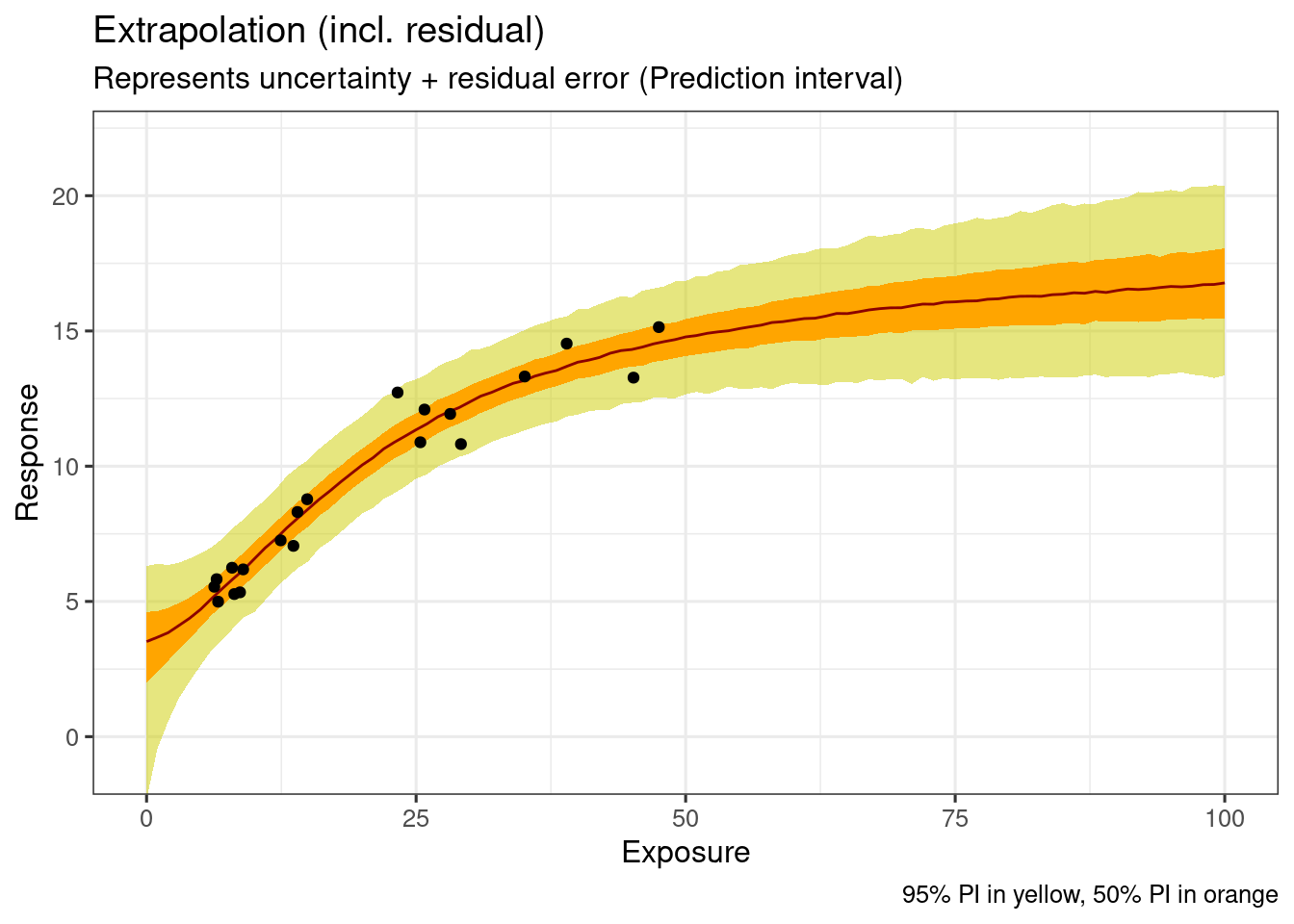
This represents uncertainty in the model parameters plus the residual error.
p(ynew|xnew, yobs)
Show the code
ggplot(
data = ersim_sigemax_med_qi,
mapping = aes(x = exposure, y = .prediction)
) +
geom_ribbon(
data = ersim_sigemax_med_qi |> filter(.width == 0.95),
mapping = aes(ymin = .prediction.lower, ymax = .prediction.upper),
fill = "yellow3",
alpha = 0.5
) +
geom_ribbon(
data = ersim_sigemax_med_qi |> filter(.width == 0.5),
mapping = aes(ymin = .prediction.lower, ymax = .prediction.upper),
fill = "orange1"
) +
geom_line(
data = ersim_sigemax_med_qi |> filter(.width == 0.5),
col = "darkred"
) +
geom_point(
data = d_sim_emax,
mapping = aes(y = response_1)
) +
coord_cartesian(ylim = c(5, 22)) +
labs(
x = "Exposure",
y = "Response",
title = "Extrapolation (incl. residual)",
subtitle = "Represents uncertainty + residual error (Prediction interval)",
caption = "95% PI in yellow, 50% PI in orange"
)
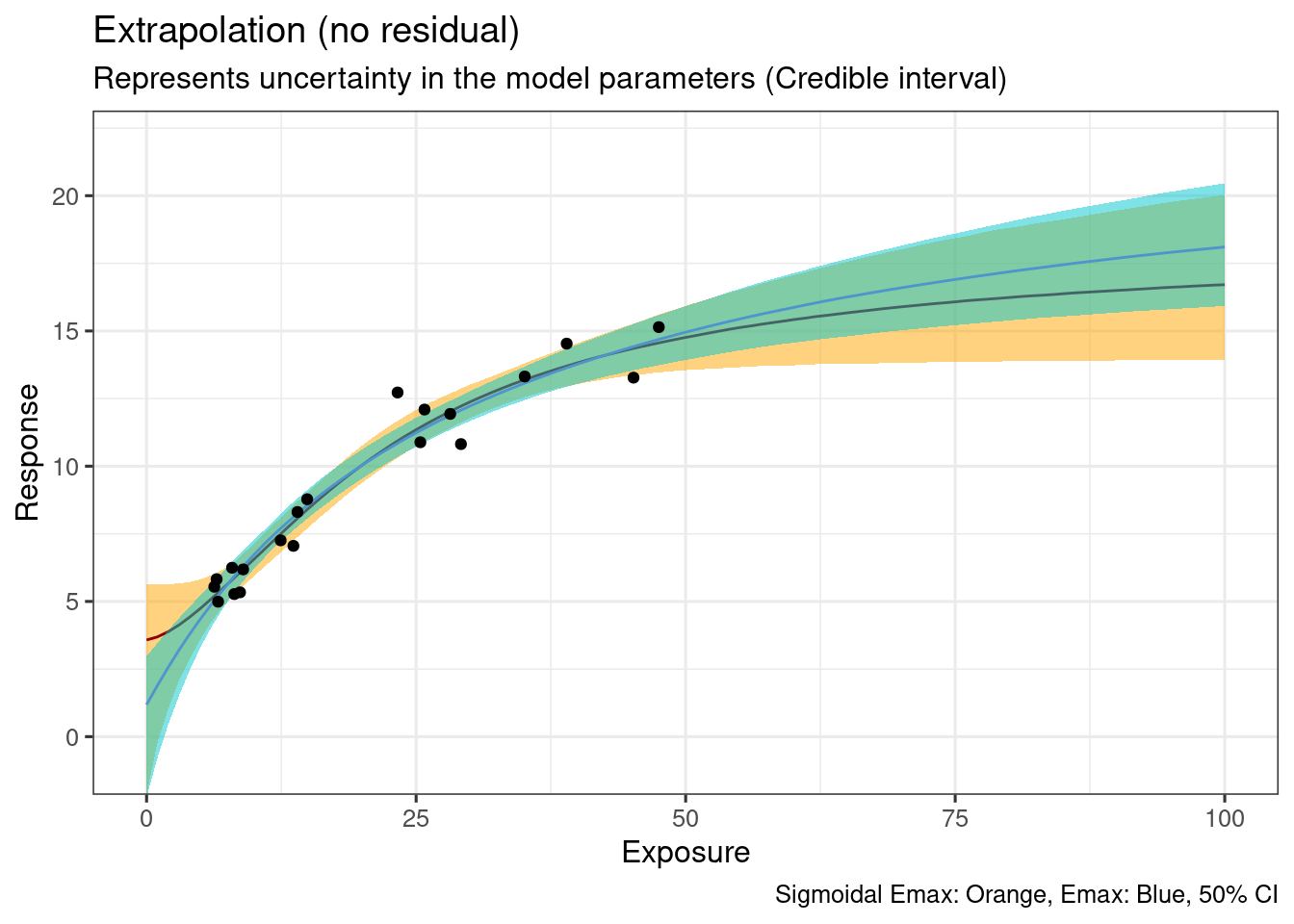
No discernible difference between the two models.
Show the code
ersim_emax <-
sim_er_new_exp(ermod_emax, new_conc_vec)
ersim_emax_med_qi <-
ersim_emax |>
calc_ersim_med_qi(qi_width = c(0.5, 0.95))
ggplot(
data = ersim_sigemax_med_qi,
mapping = aes(x = exposure, y = .epred)
) +
geom_ribbon(
data = ersim_sigemax_med_qi |> filter(.width == 0.95),
mapping = aes(ymin = .epred.lower, ymax = .epred.upper),
fill = "orange1",
alpha = 0.5
) +
geom_line(
data = ersim_sigemax_med_qi |> filter(.width == 0.95),
col = "darkred"
) +
geom_ribbon(
data = ersim_emax_med_qi |> filter(.width == 0.95),
mapping = aes(ymin = .epred.lower, ymax = .epred.upper),
fill = "turquoise3",
alpha = 0.5
) +
geom_line(
data = ersim_emax_med_qi |> filter(.width == 0.95),
col = "steelblue3"
) +
geom_point(
data = d_sim_emax,
mapping = aes(y = response_1)
) +
coord_cartesian(ylim = c(5, 22)) +
labs(
x = "Exposure",
y = "Response",
title = "Extrapolation (no residual)",
subtitle = "Represents uncertainty in the model parameters (Credible interval)",
caption = "Sigmoidal Emax: Orange, Emax: Blue, 50% CI"
)